题目内容
莱因德纸草书》是世界上最古老的数学著作之一,书中有这样的一道题目:把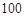 个面包分给
个面包分给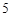 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的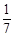 是较小的两份之和,则最小的
是较小的两份之和,则最小的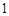 份为( )
份为( )
A.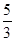 | B.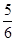 | C.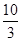 | D.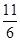 |
A
解析试题分析:由题意,设这5份分别为
 ,则有
,则有 ,
,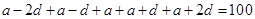 ,故
,故 ,
, ,则最小的一份
,则最小的一份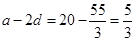 .
.
考点:等差数列的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等差数列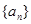 单调递增且满足
单调递增且满足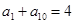 ,则
,则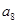 的取值范围是( )
的取值范围是( )
A.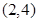 | B.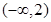 | C.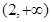 | D.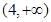 |
已知等差数列{an}中,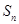 是它的前n项和.若S16>0,且
是它的前n项和.若S16>0,且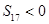 ,则当
,则当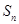 最大时n的值为( )
最大时n的值为( )
| A.8 | B.9 | C.10 | D.16 |
各项都是正数的等比数列 中,
中,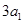 ,
,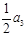 ,
,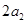 成等差数列,
成等差数列,
则 ( )
( )
A.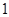 | B. | C.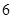 | D.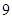 |
等差数列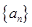 的公差
的公差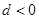 且
且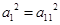 ,则数列
,则数列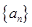 的前
的前 项和
项和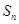 取得最大值时的项数
取得最大值时的项数 是( )
是( )
| A.5 | B.6 | C.5或6 | D.6或7 |
[2014·天津市模拟]若等差数列{an}的前5项和S5=25,且a2=3,则a7=( )
| A.12 | B.13 | C.14 | D.15 |
数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
| A.3690 | B.3660 | C.1845 | D.1830 |
已知等差数列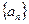 的首项为
的首项为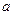 ,公差为
,公差为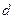 ,且方程
,且方程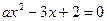 的解为
的解为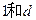 ,则数列{
,则数列{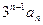 }的前n项和
}的前n项和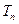 为( )
为( )
A.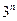 |
B.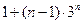 |
C.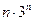 |
D.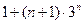 |
已知等差数列{an},且3(a3+a5)+2(a7+a10+a13)=48,则数列{an}的前13项之和为()
| A.24 |
| B.39 |
| C.104 |
| D.52 |