题目内容
(本题满分12分)
已知函数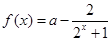 (其中常数
(其中常数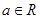 )
)
(1)判断函数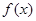 的单调性,并加以证明;
的单调性,并加以证明;
(2)如果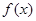 是奇函数,求实数
是奇函数,求实数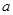 的值。
的值。
【答案】
(1) ;(2)
;(2)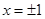 ;(3)
;(3)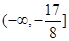 .
.
【解析】
试题分析:(1)先求解函数定义域,然后结合单调性的定义,作差变形定号,下结论得到。
(2)因为函数是奇函数则有f(-x)+f(x)=0,进而得到关于a的表达式得到求解。
解(1)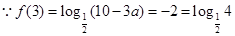
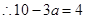 ,即
,即 (3分)
(3分)
(2)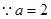 ,
,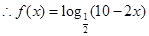
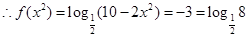
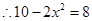 ,即
,即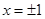 (7分)
(7分)
(3)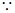 不等式
不等式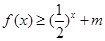 对于
对于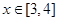 恒成立,
恒成立,
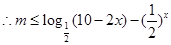 ,
,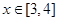 (9分)
(9分)
而函数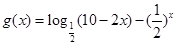 在区间
在区间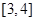 上是增函数
上是增函数
所以,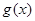 在区间
在区间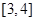 上的最小值是
上的最小值是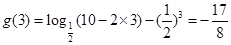 (10分)
(10分)
即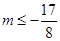 ,实数
,实数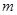 的取值范围是
的取值范围是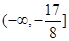 .(12分)
.(12分)
考点:本题主要考查了函数的奇偶性和单调性的运用。
点评:解决该试题的关键是能利用定义法来求解和证明函数单调性问题。作差变形定号来证明。奇偶性的判定要分为两步,一看定义域,二看解析式f(-x)与f(x)的关系。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面