题目内容
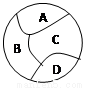
如图用n种不同颜色,给图中A、B、C、D、四块区域涂色,允许同一种颜色
涂不同区域,但相邻区域不能涂同一种颜色⑴n=3,共有多少种不同的涂法?
⑵n=5,共有多少种不同的涂法?
【答案】
(1)N = 3 × 2 ×1×1 = 6 (种). (2)N = 5 × 4 ×3×3 =180(种).
【解析】解决本小题要用乘法原理,按A、B、C、D四个区域的顺序分四个步骤进行.计算出每个区域的方法数,然后相乘即可.
解:按地图A、B、C、D四个区域的顺序依次分四步完成,,每步涂一个区域.则:
(1) 第一步, m1 = 3 种; 第二步, m2 = 2 种
第三步, m3 = 1 种; 第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 (种).
(2)n=5时 第一步, m1 = 5 种; 第二步, m2 = 4 种
第三步, m3 = 3 种; 第四步, m4 =3 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 5 × 4 ×3×3 =180(种).

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
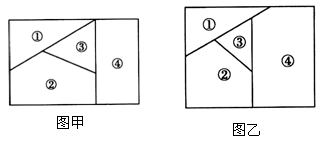
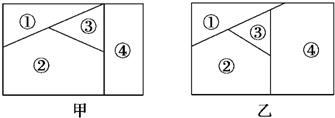 18、用n种不同颜色为下侧两块广告牌着色(如图甲、乙所示),要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用同一种颜色.
18、用n种不同颜色为下侧两块广告牌着色(如图甲、乙所示),要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用同一种颜色.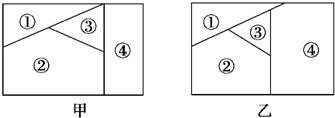 用n种不同颜色为下侧两块广告牌着色(如图甲、乙所示),要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用同一种颜色.
用n种不同颜色为下侧两块广告牌着色(如图甲、乙所示),要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用同一种颜色.