题目内容
用n种不同颜色为下列两块广告牌着色(如图甲、图乙),要求有公共边界的区域不能用同一种颜色。
(1)若n=6,为甲着色时共有多少种不同方法?
(2)若为乙着色时共有120种不同方法,求n。
(1)若n=6,为甲着色时共有多少种不同方法?
(2)若为乙着色时共有120种不同方法,求n。
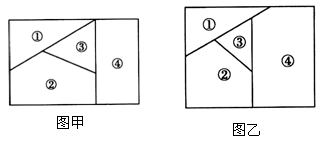
解:(1)为图甲着色时,由分步乘法计数原理知,
第1步,涂①区有6种方法;
第2步,涂②区有5种方法;
第3步,涂③区有4种方法;
第4步,涂④区有4种方法;
由分步乘法计数原理知,共有N=6×5×4×4=480(种)方法。
(2)为图乙着色时,由分步乘法计数原理知,
第1步,涂①区有n种方法;
第2步,涂②区有n-1种方法;
第3步,涂③区有n-2种方法;
第4步,涂④区有n-3种方法;
由分步乘法计数原理知,共有n(n-1)(n-2)(n-3)=120(n∈N*),
经验证n=5时,满足题意,
所以n=5。
第1步,涂①区有6种方法;
第2步,涂②区有5种方法;
第3步,涂③区有4种方法;
第4步,涂④区有4种方法;
由分步乘法计数原理知,共有N=6×5×4×4=480(种)方法。
(2)为图乙着色时,由分步乘法计数原理知,
第1步,涂①区有n种方法;
第2步,涂②区有n-1种方法;
第3步,涂③区有n-2种方法;
第4步,涂④区有n-3种方法;
由分步乘法计数原理知,共有n(n-1)(n-2)(n-3)=120(n∈N*),
经验证n=5时,满足题意,
所以n=5。

练习册系列答案
相关题目
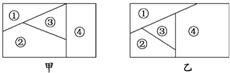 9、用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.
9、用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.
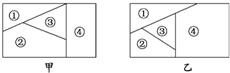 用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.
用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.