题目内容
f（x） 是定义在（-2，2）上的减函数，若f（m-1）＞f（2m-1），实数m 的取值范围
- A.m＞0
- B.
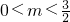
- C.-1＜m＜3
- D.
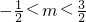
B
分析：根据f（x）是定义在（-2，2）上的减函数，f（m-1）＞f（2m-1），利用函数单调性的定义，建立不等式，即可求得实数m的取值范围．
解答：∵f（x）是定义在（-2，2）上的减函数，f（m-1）＞f（2m-1），
∴
∴
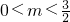
故选B．
点评：本题考查函数的单调性与奇偶性，考查学生分析解决问题的能力，属于中档题．
分析：根据f（x）是定义在（-2，2）上的减函数，f（m-1）＞f（2m-1），利用函数单调性的定义，建立不等式，即可求得实数m的取值范围．
解答：∵f（x）是定义在（-2，2）上的减函数，f（m-1）＞f（2m-1），
∴
∴
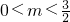
故选B．
点评：本题考查函数的单调性与奇偶性，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目