Question

8．在正方体ABCD-A₁B₁C₁D₁中，E、F分别是棱AB，BC的中点，O是底面ABCD的中心，求证EF⊥平面BB₁O．

Answer 1

分析 连结AC、BD，交于点O，由正方形性质，得AC⊥OB，由线面垂直得AC⊥BB₁，从而AC⊥平面BB₁O，由E、F分别是棱AB，BC的中点，得EF∥AC，由此能证明EF⊥平面BB₁O．

解答 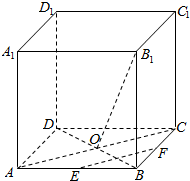证明：连结AC、BD，交于点O，
∵在正方体ABCD-A₁B₁C₁D₁中，ABCD是正方形，
∴AC⊥OB，
∵BB₁⊥底面ABCD，AC?底面ABCD，∴AC⊥BB₁，
∵OB∩BB₁=B，
∴AC⊥平面BB₁O，
∵E、F分别是棱AB，BC的中点，O是底面ABCD的中心，
∴EF∥AC，
∴EF⊥平面BB₁O．

点评 本题考查线面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．