题目内容
已知动圆M过定点P(0,m)(m>0),且与定直线l1:y=-m相切,动圆圆心M的轨迹为C,直线l2过点P交曲线C于A,B两点.(1)求曲线C的方程.(2)若l2交x轴于点S,且
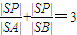 ,求l2的方程.(3)若l2的倾斜角为30°,在l1上是否存在点E使△ABE为正三角形?若能,求点E的坐标;若不能,说明理由.
,求l2的方程.(3)若l2的倾斜角为30°,在l1上是否存在点E使△ABE为正三角形?若能,求点E的坐标;若不能,说明理由.
【答案】分析:(1)依题意,曲线C是以点P为焦点,直线l1为准线的抛物线,由此可知曲线C的方程.
(2)由题意知k存在且k≠0,设l2方程为y=kx+m,代入x2=4my由消去y得x2-4mkx-4m2=0
设A(x1,y1)、B(x2,y2),则x1+x2=4mk,x1x2=-4m2,由题设条件知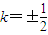 ,l2方程为
,l2方程为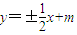 .
.
(3)由题设知l2方程为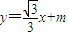 代入x2=4my,消去y得:
代入x2=4my,消去y得: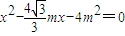
 ,
, ,假设存在点E(x,-m),使△ABE为正三角形,则|BE|=|AB|=|AE|,由此导出
,假设存在点E(x,-m),使△ABE为正三角形,则|BE|=|AB|=|AE|,由此导出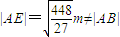 ,所以直线l上不存在点E,使得△ABE是正三角形.
,所以直线l上不存在点E,使得△ABE是正三角形.
解答:解:(1)依题意,曲线C是以点P为焦点,直线l1为准线的抛物线,
所以曲线C的方程为x2=4my
(2)由题意知k存在且k≠0
设l2方程为y=kx+m,代入x2=4my由消去y得x2-4mkx-4m2=0
设A(x1,y1)、B(x2,y2),则x1+x2=4mk,x1x2=-4m2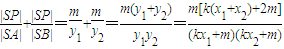 =
=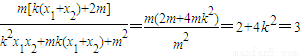
所以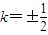 ,l2方程为
,l2方程为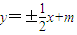
(3)由(Ⅰ)知l2方程为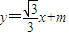 代入x2=4my,消去y得:
代入x2=4my,消去y得:
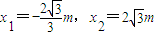 ,
,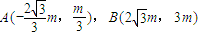
假设存在点E(x,-m),使△ABE为正三角形,则|BE|=|AB|=|AE|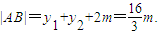
由|BE|=|AE|
即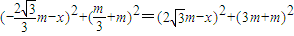 ,
,
化简得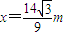
因为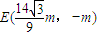 ,则
,则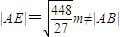
因此,直线l上不存在点E,使得△ABE是正三角形.
点评:本题考查直线和圆锥曲线的位置关系,难度较大,解题时要认真审题,注意公式的灵活运用,合理地进行等价转化.
(2)由题意知k存在且k≠0,设l2方程为y=kx+m,代入x2=4my由消去y得x2-4mkx-4m2=0
设A(x1,y1)、B(x2,y2),则x1+x2=4mk,x1x2=-4m2,由题设条件知
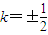 ,l2方程为
,l2方程为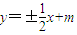 .
.(3)由题设知l2方程为
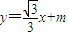 代入x2=4my,消去y得:
代入x2=4my,消去y得: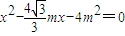
 ,
, ,假设存在点E(x,-m),使△ABE为正三角形,则|BE|=|AB|=|AE|,由此导出
,假设存在点E(x,-m),使△ABE为正三角形,则|BE|=|AB|=|AE|,由此导出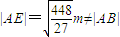 ,所以直线l上不存在点E,使得△ABE是正三角形.
,所以直线l上不存在点E,使得△ABE是正三角形.解答:解:(1)依题意,曲线C是以点P为焦点,直线l1为准线的抛物线,
所以曲线C的方程为x2=4my
(2)由题意知k存在且k≠0
设l2方程为y=kx+m,代入x2=4my由消去y得x2-4mkx-4m2=0
设A(x1,y1)、B(x2,y2),则x1+x2=4mk,x1x2=-4m2
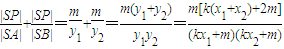 =
=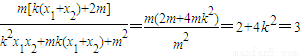
所以
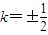 ,l2方程为
,l2方程为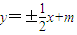
(3)由(Ⅰ)知l2方程为
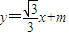 代入x2=4my,消去y得:
代入x2=4my,消去y得:
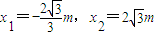 ,
,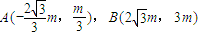
假设存在点E(x,-m),使△ABE为正三角形,则|BE|=|AB|=|AE|
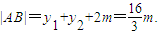
由|BE|=|AE|
即
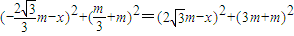 ,
,化简得
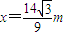
因为
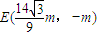 ,则
,则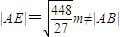
因此,直线l上不存在点E,使得△ABE是正三角形.
点评:本题考查直线和圆锥曲线的位置关系,难度较大,解题时要认真审题,注意公式的灵活运用,合理地进行等价转化.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
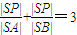 ,求l2的方程.
,求l2的方程.