题目内容
已知动圆M过定点P(0,m)(m>0),且与定直线l1:y=-m相切,动圆圆心M的轨迹为C,直线l2过点P交曲线C于A,B两点.
(Ⅰ)求曲线C的方程;
(Ⅱ)若l2交x轴于点S,且
| |SP| |
| |SA| |
| |SP| |
| |SB| |
分析:(1)圆心M的轨迹满足抛物线的方程,进而得到答案.
(2)先判定斜率存在然后得到直线的方程且与抛物线联立消去y,进而得到两根之和两根之积,然后表示出
+
整理后使其等于3可求得k的值,进而确定直线的方程.
(2)先判定斜率存在然后得到直线的方程且与抛物线联立消去y,进而得到两根之和两根之积,然后表示出
| |SP| |
| |SA| |
| |SP| |
| |SB| |
解答:解:(Ⅰ)依题意,曲线C是以点P为焦点,直线l1为准线的抛物线,
所以曲线C的方程为x2=4my
(Ⅱ)由题意知k存在且k≠0
设l2方程为y=kx+m,代入x2=4my由消去y得x2-4mkx-4m2=0
设A(x1,y1)、B(x2,y2),则x1+x2=4mk,x1x2=-4m2
+
=
+
=
=
=
=
=2+4k2=3
所以k=±
,l2方程为y=±
x+m.
所以曲线C的方程为x2=4my
(Ⅱ)由题意知k存在且k≠0
设l2方程为y=kx+m,代入x2=4my由消去y得x2-4mkx-4m2=0
设A(x1,y1)、B(x2,y2),则x1+x2=4mk,x1x2=-4m2
| |SP| |
| |SA| |
| |SP| |
| |SB| |
| m |
| y1 |
| m |
| y2 |
| m(y1+y2) |
| y1y2 |
| m[k(x1+x2)+2m] |
| (kx1+m)(kx2+m) |
=
| m[k(x1+x2)+2m] |
| k2x1x2+mk(x1+x2)+m2 |
| m(2m+4mk2) |
| m2 |
所以k=±
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查抛物线的标准方程和直线与抛物线的联立问题.圆锥曲线是高考的重点,尤其是圆锥曲线与直线的联立是每年必考的压轴问题,一定要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
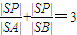 ,求l2的方程.(3)若l2的倾斜角为30°,在l1上是否存在点E使△ABE为正三角形?若能,求点E的坐标;若不能,说明理由.
,求l2的方程.(3)若l2的倾斜角为30°,在l1上是否存在点E使△ABE为正三角形?若能,求点E的坐标;若不能,说明理由.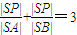 ,求l2的方程.
,求l2的方程.