题目内容
函数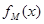 的定义域为R,且定义如下:
的定义域为R,且定义如下: (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足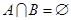 ,则函数
,则函数 的值域为
的值域为
A.
B.
C.
D.
B
解析试题分析:当x∈CR(A∪B)时,f(A∪B)(x)=0,fA(x)=0,fB(x)=0,∴F(x)=1;
同理得:当x∈B时,F(x)=1;当x∈A时,F(x)=1;故:F(x)=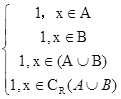 ,
,
所以F(x)的值域为B。
考点:本题考查函数的值域;子集与真子集;分段函数解析式的求法。
点评:本题主要考查了函数的值域、分段函数,属于创新型题目.这种题目要求我们迅速理解所给定义,并应用所给定义做题。理解所给定义是解题的关键。比如此题,对F(x)中的x属于什么集合进行分类讨论,利用题中新定义的函数求出f(x)的函数值,从而得到F(x)的值域即可.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下列各组函数中,表示同一个函数的是
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
设函数 的图像的交点为
的图像的交点为 ,则x0所在的区间是
,则x0所在的区间是
A. | B. | C. | D. |
函数 对任意的
对任意的 恒有
恒有 且
且 ,则
,则 ( )
( )
A. | B. | C. | D. |
在区间 上为增函数的是( )
上为增函数的是( )
A. | B. |
C. | D. |
函数 的定义域是( ).
的定义域是( ).
A. | B. | C. | D. |
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.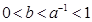 |
C. | D. |
已知函数 ,则
,则 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.既是奇函数又是偶函数 | D.非奇函数非偶函数 |
 与
与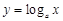 的图象可能是( )
的图象可能是( )