题目内容
已知集合A={12,14,16,18,20},B={11,13,15,17,19},在A中任取一个元素用ai(i=1,2,3,4,5)表示,在B中任取一个元素用bj(j=1,2,3,4,5)表示,则所取两数满足ai>bI的概率为 .
【答案】分析:本题是一个等可能事件的概率,试验发生包含的事件数是5×5种结果,满足条件的事件是ai>bI的情况,可以通过列举得到,列举时,a的值从小到大,要注意不要漏掉,最后根据等可能事件的概率公式得到结果.
解答:解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是5×5=25种结果,
满足条件的事件是ai>bI的情况,可以通过列举得到
当a=12,b=11;
a=14,b=11,13
a=16.b=11,13,15
a=18,b=11,13,15,17
a=20,b=11,13,15,17,19
一共有1+2+3+4+5=15种结果,
∴根据等可能事件的概率公式得到P=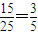 ,
,
故答案为: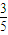
点评:本题可选等可能事件的概率,考查用列举法数出事件数,这是一个基础题,若出现在大型考试中则是一个送分题目.
解答:解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是5×5=25种结果,
满足条件的事件是ai>bI的情况,可以通过列举得到
当a=12,b=11;
a=14,b=11,13
a=16.b=11,13,15
a=18,b=11,13,15,17
a=20,b=11,13,15,17,19
一共有1+2+3+4+5=15种结果,
∴根据等可能事件的概率公式得到P=
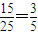 ,
,故答案为:
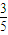
点评:本题可选等可能事件的概率,考查用列举法数出事件数,这是一个基础题,若出现在大型考试中则是一个送分题目.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目



