题目内容
已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
(1)(-1,1)(2)f(x)是偶函数(3)(-∞,0]
(1)由 得-1<x<1,所以函数f(x)的定义域为(-1,1).
得-1<x<1,所以函数f(x)的定义域为(-1,1).
(2)由f(-x)=lg(1+x)+lg(1-x)+(-x)4-2(-x)2=lg(1-x)+lg(1+x)+x4-2x2=f(x),
所以函数f(x)是偶函数.
(3)f(x)=lg(1-x)+lg(1+x)+x4-2x2=lg(1-x2)+x4-2x2,
设t=1-x2,由x∈(-1,1),得t∈(0,1].
所以y=lg(1-x2)+x4-2x2=lgt+(t2-1),t∈(0,1],
设0<t1<t2≤1,则lgt1<lgt2, <
< ,
,
所以lgt1+( -1)<lgt2+(
-1)<lgt2+( -1),
-1),
所以函数y=lgt+(t2-1)在t∈(0,1]上为增函数,
所以函数f(x)的值域为(-∞,0].
 得-1<x<1,所以函数f(x)的定义域为(-1,1).
得-1<x<1,所以函数f(x)的定义域为(-1,1).(2)由f(-x)=lg(1+x)+lg(1-x)+(-x)4-2(-x)2=lg(1-x)+lg(1+x)+x4-2x2=f(x),
所以函数f(x)是偶函数.
(3)f(x)=lg(1-x)+lg(1+x)+x4-2x2=lg(1-x2)+x4-2x2,
设t=1-x2,由x∈(-1,1),得t∈(0,1].
所以y=lg(1-x2)+x4-2x2=lgt+(t2-1),t∈(0,1],
设0<t1<t2≤1,则lgt1<lgt2,
 <
< ,
,所以lgt1+(
 -1)<lgt2+(
-1)<lgt2+( -1),
-1),所以函数y=lgt+(t2-1)在t∈(0,1]上为增函数,
所以函数f(x)的值域为(-∞,0].

练习册系列答案
相关题目
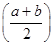 ,
,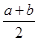 >1.
>1.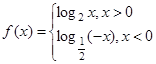 ,若
,若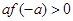 ,则实数
,则实数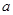 的取值范围是 ( )
的取值范围是 ( )



 ,
, 的值域是 .
的值域是 . +1,则f(lg2)+f
+1,则f(lg2)+f =________.
=________.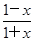 是________(填“奇”或“偶”)函数.
是________(填“奇”或“偶”)函数. f(x)=x的根从小到大构成数列{an},则a2 012=________.
f(x)=x的根从小到大构成数列{an},则a2 012=________.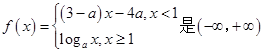 上的增函数,那么
上的增函数,那么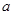 的取值范围是
的取值范围是
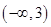


 .
.