题目内容
设f(x)=|lg x|,a,b为实数,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b满足f(a)=f(b)=2f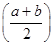 ,
,
求证:a·b=1,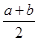 >1.
>1.
(1)求方程f(x)=1的解;
(2)若a,b满足f(a)=f(b)=2f
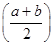 ,
,求证:a·b=1,
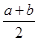 >1.
>1.(1) x=10或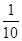 (2)见解析
(2)见解析
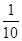 (2)见解析
(2)见解析(1)由f(x)=1得,lg x=±1,
所以x=10或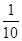 .
.
(2)证明:结合函数图象,由f(a)=f(b)可判断a∈(0,1),b∈(1,+∞),
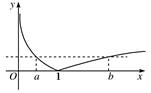
从而-lg a=lg b,从而ab=1.
又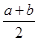 =
=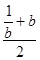 ,
,
令φ(b)=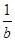 +b(b∈(1,+∞)),
+b(b∈(1,+∞)),
任取1<b1<b2,
∵φ(b1)-φ(b2)=(b1-b2)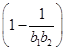 <0,
<0,
∴φ(b1)<φ(b2),
∴φ(b)在(1,+∞)上为增函数.
∴φ(b)>φ(1)=2.
∴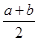 >1.
>1.
所以x=10或
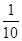 .
.(2)证明:结合函数图象,由f(a)=f(b)可判断a∈(0,1),b∈(1,+∞),

从而-lg a=lg b,从而ab=1.
又
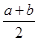 =
=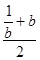 ,
,令φ(b)=
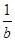 +b(b∈(1,+∞)),
+b(b∈(1,+∞)),任取1<b1<b2,
∵φ(b1)-φ(b2)=(b1-b2)
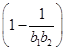 <0,
<0,∴φ(b1)<φ(b2),
∴φ(b)在(1,+∞)上为增函数.
∴φ(b)>φ(1)=2.
∴
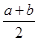 >1.
>1.
练习册系列答案
相关题目
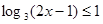 的解集为 .
的解集为 .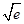 ,则a、b、c的大小关系是________.
,则a、b、c的大小关系是________.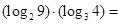 .
. 的图象和g(x)=log2x的图象的交点个数是( )
的图象和g(x)=log2x的图象的交点个数是( )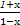 的图象( )
的图象( )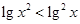 的解集是 ( )
的解集是 ( )


