题目内容
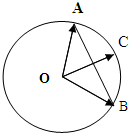如图所示，点A，B，C是圆O上的三点，线段OC与线段AB交于圆内一点，若| OC |
| OA |
| OB |
| A、0＜m+n＜1 |
| B、m+n＞1 |
| C、m+n＜-1 |
| D、-1＜m+n＜0 |
分析：不妨取∠AOB=120°，∠AOC=∠BOC=60°，此时四边形AOBC为菱形，可得
=
+
，求出m，n，从而可得到选项．
| OC |
| OA |
| OB |
解答：解：∵点A，B，C是圆O上的三点，线段OC与线段AB交于圆内一点，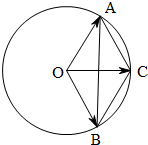
∴不妨取∠AOB=120°，∠AOC=∠BOC=60°，此时四边形AOBC为菱形，
则
=
+
，
又∵
=m
+n
，
∴m=n=1，则m+n=2，从而可排除A，C，D选项，
故选：B．
∴不妨取∠AOB=120°，∠AOC=∠BOC=60°，此时四边形AOBC为菱形，
则
| OC |
| OA |
| OB |
又∵
| OC |
| OA |
| OB |
∴m=n=1，则m+n=2，从而可排除A，C，D选项，
故选：B．
点评：本题主要考查了平面向量的几何意义，平面向量加法的平行四边形法则，平面向量基本定理，排除法解选择题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
（2013•嘉兴二模）函数y=sinωx（ω＞0）的部分图象如图所示，点A、B是最高点，点C是最低点，若△ABC是直角三角形，则ω的值为（ ）
（2012•福州模拟）函数f（x）=2cos（ωx+φ）（ω＞0，0＜φ＜π）为奇函数，该函数的部分图象如图所示，点A、B分别为该部分图象的最高点与最低点，且这两点间的距离为4
（2009•黄浦区一模）如图所示，点A、B是单位圆（圆心在原点，半径为1的圆）上两点，OA、OB与x轴正半轴所成的角分别为α和-β．
（
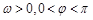）为奇函数，该函数的部分图象如图所示，点A、B分别为该部分图象的最高点与最低点，且这两点间的距离为
，则函数
图象的一条对称轴的方程为（ ）
B．
C．
D． 