题目内容
已知: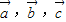 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中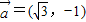
(1)若
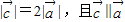 ,求
,求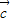 的坐标;
的坐标;(2)若
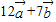 与
与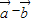 垂直,且
垂直,且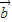 与
与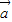 的夹角为120°,求
的夹角为120°,求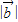 .
.
【答案】分析:(1)令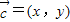 ,由
,由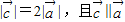 建立关于
建立关于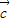 的坐标的方程,求出它的坐标即可;
的坐标的方程,求出它的坐标即可;
(2)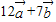 与
与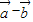 垂直,则它们的内积为0,由此方程结合
垂直,则它们的内积为0,由此方程结合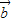 与
与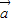 的夹角为120,求出向量的模,
的夹角为120,求出向量的模,
解答:解:(1)令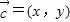 ,由
,由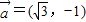 ,
,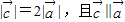 得
得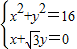
解得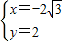 或
或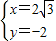
故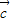 的坐标为
的坐标为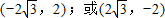
(2)∵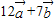 与
与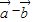 垂直
垂直
∴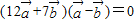 ,
,
即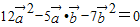
又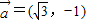 ,
,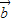 与
与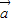 的夹角为120,
的夹角为120,
得48+5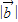
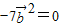 解得
解得
点评:本题考查平面向量的综合题,解答本题关键是熟练掌握向量的模的坐标表示,向量共线的坐标表示,两向量垂直的条件,向量的数量积公式,本题涉及到了向量的主要运算,综合性强,是向量中非常典型的综合题,此题也是近几年高考中对向量考查时出现率最高的形式.本题常因忘记等价条件导致无法转化,致使解题失败,平坦学习时一定要注意积累基础知识,记牢,记准.
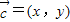 ,由
,由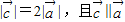 建立关于
建立关于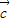 的坐标的方程,求出它的坐标即可;
的坐标的方程,求出它的坐标即可;(2)
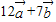 与
与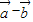 垂直,则它们的内积为0,由此方程结合
垂直,则它们的内积为0,由此方程结合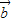 与
与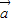 的夹角为120,求出向量的模,
的夹角为120,求出向量的模,解答:解:(1)令
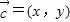 ,由
,由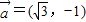 ,
,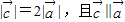 得
得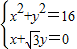
解得
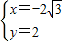 或
或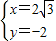
故
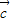 的坐标为
的坐标为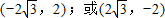
(2)∵
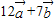 与
与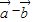 垂直
垂直∴
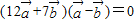 ,
,即
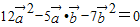
又
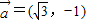 ,
,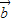 与
与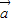 的夹角为120,
的夹角为120,得48+5
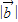
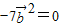 解得
解得
点评:本题考查平面向量的综合题,解答本题关键是熟练掌握向量的模的坐标表示,向量共线的坐标表示,两向量垂直的条件,向量的数量积公式,本题涉及到了向量的主要运算,综合性强,是向量中非常典型的综合题,此题也是近几年高考中对向量考查时出现率最高的形式.本题常因忘记等价条件导致无法转化,致使解题失败,平坦学习时一定要注意积累基础知识,记牢,记准.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 都是同一平面内的非零向量,则下列说法中:
都是同一平面内的非零向量,则下列说法中: ,则
,则 一定与
一定与 共线; (2)若
共线; (2)若 ,则
,则 ;
; ,则
,则 一定不能等于
一定不能等于 ,其中正确说法的个数是( )
,其中正确说法的个数是( ) 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中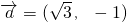
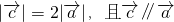 ,求
,求 的坐标;
的坐标;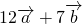 与
与 垂直,且
垂直,且 与
与 的夹角为1200,,求
的夹角为1200,,求 .
.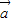 ,
,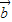 是同一平面内的两个向量,其中
是同一平面内的两个向量,其中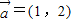 ,
,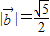 且
且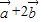 与
与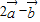 垂直,(1)求
垂直,(1)求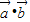 ; (2)求|
; (2)求|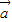 -
-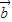 |.
|.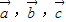 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
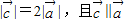 ,求
,求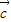 的坐标;
的坐标;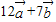 与
与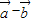 垂直,且
垂直,且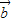 与
与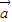 的夹角为120°,求
的夹角为120°,求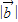 .
.