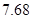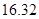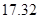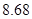题目内容
将长为1 的棒任意地折成三段,求三段的长度都不超过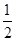 的概率.
的概率.
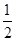 的概率.
的概率. 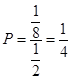
利用几何概型概率计算公式可知,设第一段的长度为 x,第二段的长度为 y,第三段的长度为 1-x-y,则基本事件组所对应的几何区域可表示为
 ,事件“三段的长度都不超过
,事件“三段的长度都不超过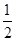 ”所对应的几何区域可表示为
”所对应的几何区域可表示为
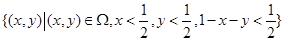 ,即图中最中间三角形区域,此区域面积:为
,即图中最中间三角形区域,此区域面积:为 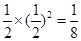 利用面积比求解概率值即可。
利用面积比求解概率值即可。
解:设第一段的长度为 x,第二段的长度为 y,第三段的长度为 1-x-y, 1分
则基本事件组所对应的几何区域可表示为
 ,即图中黄色区域,此区域面积为
,即图中黄色区域,此区域面积为 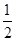 4分
4分
事件“三段的长度都不超过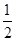 ”所对应的几何区域可表示为
”所对应的几何区域可表示为
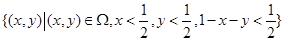 ,即图中最中间三角形区域,此区域面积:为
,即图中最中间三角形区域,此区域面积:为 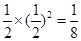 10分
10分
此时事件“三段的长度都不超过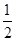 的概率为
的概率为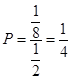 12分
12分
 ,事件“三段的长度都不超过
,事件“三段的长度都不超过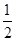 ”所对应的几何区域可表示为
”所对应的几何区域可表示为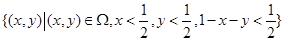 ,即图中最中间三角形区域,此区域面积:为
,即图中最中间三角形区域,此区域面积:为 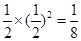 利用面积比求解概率值即可。
利用面积比求解概率值即可。解:设第一段的长度为 x,第二段的长度为 y,第三段的长度为 1-x-y, 1分
则基本事件组所对应的几何区域可表示为
 ,即图中黄色区域,此区域面积为
,即图中黄色区域,此区域面积为 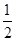 4分
4分事件“三段的长度都不超过
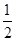 ”所对应的几何区域可表示为
”所对应的几何区域可表示为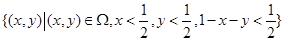 ,即图中最中间三角形区域,此区域面积:为
,即图中最中间三角形区域,此区域面积:为 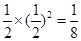 10分
10分此时事件“三段的长度都不超过
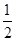 的概率为
的概率为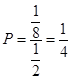 12分
12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上随机取一实数
上随机取一实数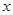 ,则该实数
,则该实数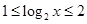 的概率为 .
的概率为 .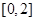 内任取两个数
内任取两个数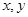 ,则“
,则“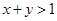 ”的概率是 。
”的概率是 。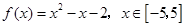 ,在定义域内任取一点
,在定义域内任取一点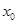 ,使
,使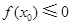 的概率是____;
的概率是____;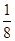
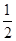
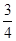





 ,任取一点
,任取一点 ,使
,使 的概率( )
的概率( )