题目内容
在各项为正的数列{an}中,数列的前n项和Sn满足Sn=
(an+
)
(1)求a1,a2,a3;
(2)由(1)结果猜想出数列{an}的通项公式(不用证明);
(3)求Sn.
| 1 |
| 2 |
| 1 |
| an |
(1)求a1,a2,a3;
(2)由(1)结果猜想出数列{an}的通项公式(不用证明);
(3)求Sn.
分析:(1)由题设条件,分别令n=1,2,3,能够求出a1,a2,a3.
(2)由(1)猜想数列{an}的通项公式:an=
-
(n∈N*),
(3)由(2)可得:Sn=a1+a2+…+an=1+
-1+
-
+…+
-
利用回头消去法化简即得.
(2)由(1)猜想数列{an}的通项公式:an=
| n |
| n-1 |
(3)由(2)可得:Sn=a1+a2+…+an=1+
| 2 |
| 3 |
| 2 |
| n |
| n-1 |
解答:解:(1)由Sn=
(an+
)(n∈N*),
令n=1得a1=
(a1+
)⇒a1=1,
令n=2得a1+a2=
(a2+
)⇒a2=
-1,
令n=3得a1+a2+a3=
(a3+
)⇒a3=
-
,
同样地,可求得a4=
-
.
故a1=1,a2=
-1,a3=
-
,a4=
-
…(6分)
(2)根据(1)猜想:an=
-
(n∈N*)…(10分)
(3)由(2)可得:
Sn=a1+a2+…+an=1+
-1+
-
+…+
-
=
(n∈N*)…(14分)
| 1 |
| 2 |
| 1 |
| an |
令n=1得a1=
| 1 |
| 2 |
| 1 |
| a1 |
令n=2得a1+a2=
| 1 |
| 2 |
| 1 |
| a2 |
| 2 |
令n=3得a1+a2+a3=
| 1 |
| 2 |
| 1 |
| a3 |
| 3 |
| 2 |
同样地,可求得a4=
| 4 |
| 3 |
故a1=1,a2=
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
(2)根据(1)猜想:an=
| n |
| n-1 |
(3)由(2)可得:
Sn=a1+a2+…+an=1+
| 2 |
| 3 |
| 2 |
| n |
| n-1 |
| n |
点评:本小题主要考查归纳推理、数列递推关系式的应用、数列的求和等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
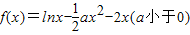
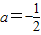 且关于x的方程
且关于x的方程 在[1,4]上恰有两个不相等的实数根,求实数b的取值范围;
在[1,4]上恰有两个不相等的实数根,求实数b的取值范围;