题目内容
(1)极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为 ;(2)如果关于x的不等式|x-3|-|x-4|<a的解集不是空集,则实数a的取值范围是 ;
(3)如图,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,则AC= .

【答案】分析:(1)把极坐标方程化为直角坐标方程,求出两圆心的坐标,再利用两点间的距离公式求出圆心距.
(2)由绝对值的意义可得|x-3|-|x-4|的最小值为-1,若关于x的不等式|x-3|-|x-4|<a的解集不是空集,
则应有a>-1.
(3)由于AE平分∠CAB,设∠EAB=∠CAE=θ,则∠ACB=θ,三角形ACE中,利用正弦定理求出AC的值.
解答:解:(1)ρ=2cosθ 即 ρ2=2ρcosθ,x2+y2=2x,即 (x-1)2+y2=1,
表示以M(1,0)为圆心、半径等于1的圆.
ρ=sinθ 即 ρ2=ρsinθ,x2+y2=y,即 ,表示以N(0,
,表示以N(0, )为圆心、半径等于
)为圆心、半径等于 的圆.
的圆.
两个圆的圆心距为MN= =
=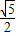 .
.
故答案为 .
.
(2)由于|x-3|-|x-4|表示数轴上的x对应点到3对应点的距离减去数轴上的x对应点到4对应点的距离,
故|x-3|-|x-4|的最小值为-1,若关于x的不等式|x-3|-|x-4|<a的解集不是空集,则应有a>-1.
故答案为a>-1.
(3)由于AE平分∠CAB,设∠EAB=∠CAE=θ,则∠ACB=θ.
直角三角形ABC中,由于∠ABC= ,∴∠EAB+∠CAE+∠ACB=
,∴∠EAB+∠CAE+∠ACB= ,∴3θ=
,∴3θ= ,θ=
,θ= .
.
三角形ACE中,∠AEC=π-∠EAC-∠ECA=π-2θ=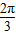 ,再由正弦定理可得
,再由正弦定理可得 ,
,
即 ,解得 AC=2
,解得 AC=2 ,
,
故答案为 2 .
.
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,绝对值不等式的解法,正弦定理的应用,属于中档题.
(2)由绝对值的意义可得|x-3|-|x-4|的最小值为-1,若关于x的不等式|x-3|-|x-4|<a的解集不是空集,
则应有a>-1.
(3)由于AE平分∠CAB,设∠EAB=∠CAE=θ,则∠ACB=θ,三角形ACE中,利用正弦定理求出AC的值.
解答:解:(1)ρ=2cosθ 即 ρ2=2ρcosθ,x2+y2=2x,即 (x-1)2+y2=1,
表示以M(1,0)为圆心、半径等于1的圆.
ρ=sinθ 即 ρ2=ρsinθ,x2+y2=y,即
 ,表示以N(0,
,表示以N(0, )为圆心、半径等于
)为圆心、半径等于 的圆.
的圆.两个圆的圆心距为MN=
 =
=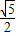 .
.故答案为
 .
.(2)由于|x-3|-|x-4|表示数轴上的x对应点到3对应点的距离减去数轴上的x对应点到4对应点的距离,
故|x-3|-|x-4|的最小值为-1,若关于x的不等式|x-3|-|x-4|<a的解集不是空集,则应有a>-1.
故答案为a>-1.
(3)由于AE平分∠CAB,设∠EAB=∠CAE=θ,则∠ACB=θ.
直角三角形ABC中,由于∠ABC=
 ,∴∠EAB+∠CAE+∠ACB=
,∴∠EAB+∠CAE+∠ACB= ,∴3θ=
,∴3θ= ,θ=
,θ= .
.三角形ACE中,∠AEC=π-∠EAC-∠ECA=π-2θ=
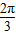 ,再由正弦定理可得
,再由正弦定理可得 ,
,即
 ,解得 AC=2
,解得 AC=2 ,
,故答案为 2
 .
.点评:本题主要考查把极坐标方程化为直角坐标方程的方法,绝对值不等式的解法,正弦定理的应用,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 (1)极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为
(1)极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为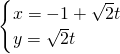 的直线位置关系是________
的直线位置关系是________