题目内容
(1)极坐标方程分别为ρ=2cosθ的圆与参数方程为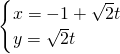 的直线位置关系是________
的直线位置关系是________
(2)一个等腰三角形ABC的底边AC的长为6,△ABC的外接圆的半径长为5,则△ABC的面积是________.
解:(1)圆ρ=2cosθ的直角坐标方程为:x2+y2=2x,即(x-1)2+y2=1
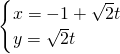 化为普通方程为:x-y+1=0
化为普通方程为:x-y+1=0
圆心到直线的距离为: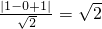
∵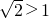
∴直线与圆相离
故答案为:相离.
(2)因为等腰三角形ABC的底边AC的长为6,△ABC的外接圆的半径长为5
∴当角B是锐角时,根据外接圆的性质知圆心o到AC边的中点的距离是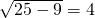
∴底边上的高是4+5=9,
∴三角形的面积是 =27
=27
当角B是钝角时,OA=5,OC=5
根据勾股定理知O到底边的距离是4,
∴三角形底边上的高是1,
∴三角形的面积是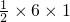 =3
=3
综上可知三角形的面积是3或27
故答案为:3或27
分析:(1)先化极坐标方程为直角坐标方程,参数方程化为普通方程,利用圆心到直线的距离与半径比较即可得结论.
(2)根据所给的三角形的外接圆的半径和边长,构造直角三角形,做出三角形的底边上的高,做出面积,注意题目中的三角形可以有两解,不要漏解.
点评:本题以极坐标方程,参数方程为载体,考查圆的方程,直线的方程,考查直线与圆的位置关系,和三角形的有关运算,本题属于基础题.
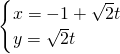 化为普通方程为:x-y+1=0
化为普通方程为:x-y+1=0圆心到直线的距离为:
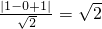
∵
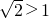
∴直线与圆相离
故答案为:相离.
(2)因为等腰三角形ABC的底边AC的长为6,△ABC的外接圆的半径长为5
∴当角B是锐角时,根据外接圆的性质知圆心o到AC边的中点的距离是
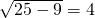
∴底边上的高是4+5=9,
∴三角形的面积是
 =27
=27当角B是钝角时,OA=5,OC=5
根据勾股定理知O到底边的距离是4,
∴三角形底边上的高是1,
∴三角形的面积是
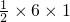 =3
=3综上可知三角形的面积是3或27
故答案为:3或27
分析:(1)先化极坐标方程为直角坐标方程,参数方程化为普通方程,利用圆心到直线的距离与半径比较即可得结论.
(2)根据所给的三角形的外接圆的半径和边长,构造直角三角形,做出三角形的底边上的高,做出面积,注意题目中的三角形可以有两解,不要漏解.
点评:本题以极坐标方程,参数方程为载体,考查圆的方程,直线的方程,考查直线与圆的位置关系,和三角形的有关运算,本题属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为
(1)极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为