题目内容
[理]一个袋子里装有编号为1,2,…,12的12个相同大小的小球,其中1到6号球是红色球,其余为黑色球.若从中任意摸出一个球,记录它的颜色和号码后再放回到袋子里,然后再摸出一个球,记录它的颜色和号码,则两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是( )A.
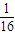
B.
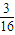
C.

D.
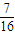
【答案】分析:首先分析题目求两次摸出的球都是红球且至少有一个球的号码是偶数的概率.分析到题目是有放回的抽取,故可以得到抽取两次总共的取法.对于至少问题,需要根据反面思想.先求出两次摸出的球都是红球的取法,再求出反面两次取到红球没有一次是偶数的种数.前者减去后者即可得到两次摸出的球都是红球且至少有一次号码是偶数的种数,除以总的可能性即可得到答案.
解答:解:据题意由于是有放回地抽取,故共有12×12=144种取法,
其中两次取到红球的情况有6×6=36种可能,又两次取到红球没有一次是偶数的种数为3×3=9
所以两次摸出的球都是红球且至少有一次号码是偶数的情况共有6×6-3×3=27种可能,
故其概率为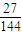 =
=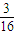 .
.
故选B.
点评:此题主要考查等可能事件的概率的问题,其中涉及到求“至少”的问题,用到求反面的思想.概率问题在高考中属于必考内容,且考查题型多为中档题型,同学们需要掌握.
解答:解:据题意由于是有放回地抽取,故共有12×12=144种取法,
其中两次取到红球的情况有6×6=36种可能,又两次取到红球没有一次是偶数的种数为3×3=9
所以两次摸出的球都是红球且至少有一次号码是偶数的情况共有6×6-3×3=27种可能,
故其概率为
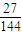 =
=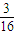 .
.故选B.
点评:此题主要考查等可能事件的概率的问题,其中涉及到求“至少”的问题,用到求反面的思想.概率问题在高考中属于必考内容,且考查题型多为中档题型,同学们需要掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



