题目内容
对函数f(x)=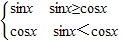 有下列命题:
有下列命题:①f(x)的值域为[-1,1];
②当且仅当x=2kл+
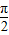 ,k∈Z时,该函数取最大值1;
,k∈Z时,该函数取最大值1;③f(x)是以л为最小正周期的函数;
④当且仅当2kл+л<x<2kл+
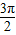 ,k∈Z时,f(x)<0.
,k∈Z时,f(x)<0.其中正确的是( )
A.①②
B.②③
C.③
D.④
【答案】分析:由题意可得:函数 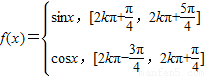 ,再根据周期函数的定义结合其图象可得函数的周期等性质即可.
,再根据周期函数的定义结合其图象可得函数的周期等性质即可.
解答: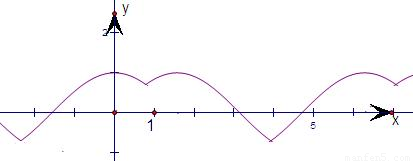 解:由题意可得:函数
解:由题意可得:函数 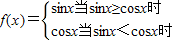 ,即
,即 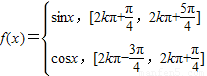 ,作出其图象如图,从图象上可以看出:
,作出其图象如图,从图象上可以看出:
①sinx≥cosx,∴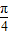 +2kπ≤x≤
+2kπ≤x≤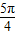 +2kπ
+2kπ
∵sinx<cosx,∴-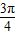 +2kπ<x<
+2kπ<x<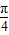 +2kπ
+2kπ
∴f(x)=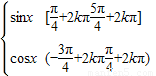 ,∴f(x)的值域为[-
,∴f(x)的值域为[-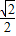 ,1]
,1]
②当x=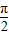 +2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.
+2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.
∵f(x+π)=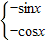 ≠f(x)
≠f(x)
③∴f(x)不是以π为最小正周期的周期函数,
④当f(x)<0时,2kπ+π<x<2kπ+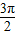 (k∈Z)
(k∈Z)
综上所述,正确的④,
故选D.
点评:本提主要考查了正弦函数及余弦函数图象的应用,利用定义先找出函数的图象,结合图象及三角函数的图象来判断函数的性质,体现了数形结合的思想.
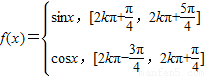 ,再根据周期函数的定义结合其图象可得函数的周期等性质即可.
,再根据周期函数的定义结合其图象可得函数的周期等性质即可.解答:
 解:由题意可得:函数
解:由题意可得:函数 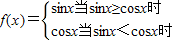 ,即
,即 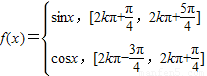 ,作出其图象如图,从图象上可以看出:
,作出其图象如图,从图象上可以看出:①sinx≥cosx,∴
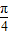 +2kπ≤x≤
+2kπ≤x≤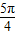 +2kπ
+2kπ∵sinx<cosx,∴-
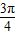 +2kπ<x<
+2kπ<x<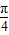 +2kπ
+2kπ∴f(x)=
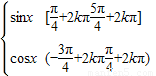 ,∴f(x)的值域为[-
,∴f(x)的值域为[-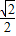 ,1]
,1]②当x=
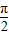 +2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.
+2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.∵f(x+π)=
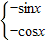 ≠f(x)
≠f(x)③∴f(x)不是以π为最小正周期的周期函数,
④当f(x)<0时,2kπ+π<x<2kπ+
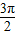 (k∈Z)
(k∈Z)综上所述,正确的④,
故选D.
点评:本提主要考查了正弦函数及余弦函数图象的应用,利用定义先找出函数的图象,结合图象及三角函数的图象来判断函数的性质,体现了数形结合的思想.

练习册系列答案
相关题目
