题目内容
解关 于x的 不 等 式: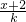 >
>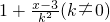 ,并回答下列 问 题:
,并回答下列 问 题:
(1)若 解 集 为 {x|x>3},求k的值.
(2)若x=3在 解 集 中,求k的 取 值 范 围.
解:原不等式可化为: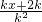 >
>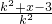 ,又k≠0,∴k2>0,
,又k≠0,∴k2>0,
∴原不等式等价于kx+2k>k2+x-3,即(k-1)x>k2-2k-3,当k>1时,x>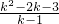 ,
,
当k<1时,x<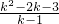 ,当k=1时,x∈R.
,当k=1时,x∈R.
(1)依题意得: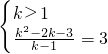 ,解得 k=5.
,解得 k=5.
(2)依题意得: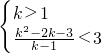 ,或
,或 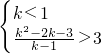 ,或k=1,
,或k=1,
解得 0<k<5.
分析:原不等式等价于 当k>1时,x>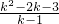 ,当k<1时,x<
,当k<1时,x<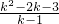 ,当k=1时,x∈R.
,当k=1时,x∈R.
(1)依题意得: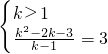 ,解得 k值.
,解得 k值.
(2)依题意得: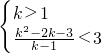 ,或
,或 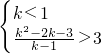 ,或k=1,解得k的取值范.
,或k=1,解得k的取值范.
点评:本题考查一元二次不等式的解法,元素与集合的关系,体现了分类讨论的数学思想,由x=3在 解 集 中,得到
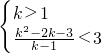 或
或 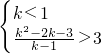 或k=1,是解题的关键.
或k=1,是解题的关键.
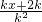 >
>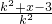 ,又k≠0,∴k2>0,
,又k≠0,∴k2>0,∴原不等式等价于kx+2k>k2+x-3,即(k-1)x>k2-2k-3,当k>1时,x>
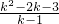 ,
,当k<1时,x<
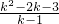 ,当k=1时,x∈R.
,当k=1时,x∈R.(1)依题意得:
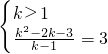 ,解得 k=5.
,解得 k=5.(2)依题意得:
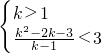 ,或
,或 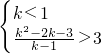 ,或k=1,
,或k=1,解得 0<k<5.
分析:原不等式等价于 当k>1时,x>
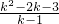 ,当k<1时,x<
,当k<1时,x<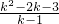 ,当k=1时,x∈R.
,当k=1时,x∈R.(1)依题意得:
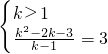 ,解得 k值.
,解得 k值.(2)依题意得:
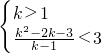 ,或
,或 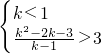 ,或k=1,解得k的取值范.
,或k=1,解得k的取值范.点评:本题考查一元二次不等式的解法,元素与集合的关系,体现了分类讨论的数学思想,由x=3在 解 集 中,得到
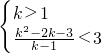 或
或 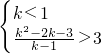 或k=1,是解题的关键.
或k=1,是解题的关键. 
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目