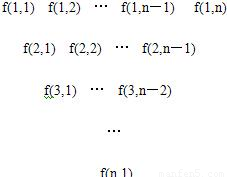��Ŀ����
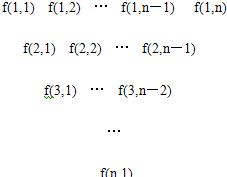 һ�����������������·�ʽ���ɣ���һ������д��n��n��4������������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf��i��j����
һ�����������������·�ʽ���ɣ���һ������д��n��n��4������������һ�е�ÿ�����������м����·�д��������֮�ͣ��õ���һ�У��������ƣ��������е�i�еĵ�j����Ϊf��i��j������1���������е�i ��1��i��n-3���е������γɵȲ����У�
��֤����i+1�е���Ҳ���γɵȲ����У�
��2����֪f��1��j��=4j����f��i��1������i�ı���ʽ��
��3���ڣ�2���������£���f��i��1��=��i+1����ai-1����bi=
| 1 |
| aiai+1 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
��������1����֪�����е�i+1�е���������������е�ͨ��Ϊf��i+1��j�������ɵȲ����ж���֤����
��2��f��1��j��=4j�ɣ�1��֪����2�е���Ҳ���γɵȲ����У��������ƿ���⣻
��3����f��i��1��=��i+1����ai-1�����ɵ�ai�������bi����g��i��=2i�����sn����̽��
��2��f��1��j��=4j�ɣ�1��֪����2�е���Ҳ���γɵȲ����У��������ƿ���⣻
��3����f��i��1��=��i+1����ai-1�����ɵ�ai�������bi����g��i��=2i�����sn����̽��
����⣺��1�������е�i+1�е���������������е�ͨ��Ϊf��i+1��j����
��������ɵ�f��i+1��j+1��-f��i+1��j��
=[f��i��j+1��+f��i��j+2��]-[f��i��j��+f��i��j+1��]
=f��i��j+2��-f��i��j��=2d������dΪ��i��������ɵ����еĹ����4�֣�
��2����f��1��j��=4j
���һ�е������γɵȲ����У�
�ɣ�1��֪����2�е���Ҳ���γɵȲ����У��������ƣ�
��֪��������һ�е�����������3���������γɵȲ����У�
���i�е�������Ϊdi����di+1=2di����di=d1��2i-1=4��2i-1=2i+1
����f��i��1��=f��i-1��1��+f��i-1��2��=2f��i-1��1��+2i
=2[2f��i-2��1��+2i-1]+2i=22f��i-2��1��+2��2i
=2i-1f��1��1��+��i-1����2i=2i-1��4+��i-1����2i=2i+1+��i-1����2i=��i+1����2i��10�֣�
��3����f��i��1��=��i+1����ai-1�����ɵ�ai=
+1=2i+1
����bi=
=
=
(
-
)
��g��i��=2i����big(i)=
-
������Sn=
-
��
Ҫʹ��Sn��m����
-
��m��ֻҪ
��
-m=
��
��m��(
��
)����0��1-3m��
������ֻҪ2n+1+1��
��
��ֻҪn��log2(
-1)-1�����Կ�������=log2(
-1)-1
��n����ʱ������Sn��m�������ʺ������һ������Ϊg��x��=2x��16�֣�
��������ɵ�f��i+1��j+1��-f��i+1��j��
=[f��i��j+1��+f��i��j+2��]-[f��i��j��+f��i��j+1��]
=f��i��j+2��-f��i��j��=2d������dΪ��i��������ɵ����еĹ����4�֣�
��2����f��1��j��=4j
���һ�е������γɵȲ����У�
�ɣ�1��֪����2�е���Ҳ���γɵȲ����У��������ƣ�
��֪��������һ�е�����������3���������γɵȲ����У�
���i�е�������Ϊdi����di+1=2di����di=d1��2i-1=4��2i-1=2i+1
����f��i��1��=f��i-1��1��+f��i-1��2��=2f��i-1��1��+2i
=2[2f��i-2��1��+2i-1]+2i=22f��i-2��1��+2��2i
=2i-1f��1��1��+��i-1����2i=2i-1��4+��i-1����2i=2i+1+��i-1����2i=��i+1����2i��10�֣�
��3����f��i��1��=��i+1����ai-1�����ɵ�ai=
| f(i��1) |
| i+1 |
����bi=
| 1 |
| aiai+1 |
| 1 |
| (2i+1)(2i+1+1) |
| 1 |
| 2i |
| 1 |
| 2i+1 |
| 1 |
| 2i+1+1 |
��g��i��=2i����big(i)=
| 1 |
| 2i+1 |
| 1 |
| 2i+1+1 |
| 1 |
| 3 |
| 1 |
| 2n+1+1 |
| 1 |
| 3 |
Ҫʹ��Sn��m����
| 1 |
| 3 |
| 1 |
| 2n+1+1 |
| 1 |
| 2n+1+1 |
| 1 |
| 3 |
| 1-3m |
| 3 |
��m��(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 1-3m |
��ֻҪn��log2(
| 3 |
| 1-3m |
| 3 |
| 1-3m |
��n����ʱ������Sn��m�������ʺ������һ������Ϊg��x��=2x��16�֣�
����������ͨ����������Ȳ����е�ͨ�ʽ�����壮

��ϰ��ϵ�д�
�����Ŀ
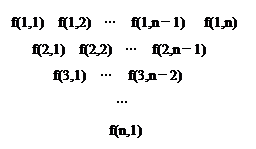
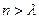 ʱ������Sn >m.
ʱ������Sn >m.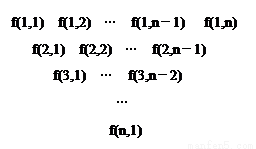 Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�
Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�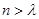 ʱ������Sn >m.
ʱ������Sn >m. Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�n��ʱ������Sn >m.
Sn=b1g(1)+b2g(2)+��+bng(n)�����Ҷ��������m��(,)��������ʵ����ʹ�õ�n��ʱ������Sn >m.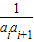 ������һ������f��x����ʹ��Sn=b1g��1��+b2g��2��+��+bng��n����
������һ������f��x����ʹ��Sn=b1g��1��+b2g��2��+��+bng��n���� ���Ҷ��������m�ʣ�
���Ҷ��������m�ʣ� ��
�� ����������ʵ����?��ʹ�õ�n��?��ʱ������Sn��m��
����������ʵ����?��ʹ�õ�n��?��ʱ������Sn��m��