题目内容
设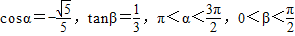 ,求α-β的值.
,求α-β的值.
【答案】分析:由cosα的值及α的范围,利用同角三角函数间的基本关系求出sinα的值,进而求出tanα的值,利用两角和与差的正切函数公式化简tan(α-β)后,将求出的tanα以及已知tanβ的值代入求出tan(α-β)的值,由α和β的范围求出α-β的范围,利用特殊角的三角函数值即可求出α-β的度数.
解答:解:∵cosα=-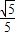 ,π<α<
,π<α<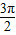 ,
,
∴sinα=-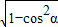 =-
=-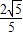 ,
,
∴tanα=2,又tanβ= ,
,
∴tan(α-β)=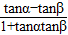 =
=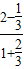 =1,
=1,
∵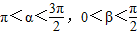 ,
,
∴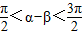 ,
,
∴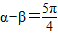 .
.
点评:此题考查了两角和与差的正切函数公式,同角三角函数间的基本关系,以及特殊角的三角函数值,熟练掌握公式是解本题的关键,同时注意角度的范围.
解答:解:∵cosα=-
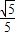 ,π<α<
,π<α<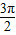 ,
,∴sinα=-
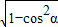 =-
=-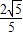 ,
,∴tanα=2,又tanβ=
 ,
,∴tan(α-β)=
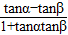 =
=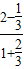 =1,
=1,∵
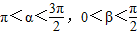 ,
,∴
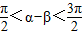 ,
,∴
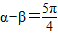 .
.点评:此题考查了两角和与差的正切函数公式,同角三角函数间的基本关系,以及特殊角的三角函数值,熟练掌握公式是解本题的关键,同时注意角度的范围.

练习册系列答案
相关题目

 ABC中,设
ABC中,设 ,求A的值。
,求A的值。 与函数
与函数 。
。 ,
, 的图像在点
的图像在点 处有公共的切线,求实数
处有公共的切线,求实数 的值;
的值; ,求函数
,求函数 的值。
的值。