题目内容
下列从集合A到集合B的对应f是映射的是
- A.

- B.
- C.
- D.
D
分析:逐一分析各个选项中的对应是否满足映射的概念,即前一个集合中的每一个元素在后一个集合中是否都有唯一确定的元素和它对应.
解答:如果一个集合中的任何元素在另一个集合中都有唯一确定的一个元素和它对应,则此对应构成映射.
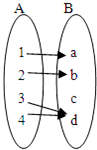
故选项D构成映射,
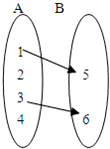
对于选项A:集合B中4在集合A中对应两个数1,2,故此对应不是映射.
对于选项B:不能构成映射,因为前边的集合中的元素2,4在后一个集合中没有元素和它对应,故此对应不是映射.
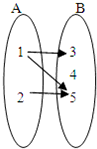
对于选项C:集合B中5在集合A中对应两个数1,2,所以C是错误的.
故选D.
点评:本题考查映射的概念,即一个集合中的任何元素在另一个集合中都有唯一确定的一个元素和它对应,则此对应构成映射.
分析:逐一分析各个选项中的对应是否满足映射的概念,即前一个集合中的每一个元素在后一个集合中是否都有唯一确定的元素和它对应.
解答:如果一个集合中的任何元素在另一个集合中都有唯一确定的一个元素和它对应,则此对应构成映射.
故选项D构成映射,
对于选项A:集合B中4在集合A中对应两个数1,2,故此对应不是映射.
对于选项B:不能构成映射,因为前边的集合中的元素2,4在后一个集合中没有元素和它对应,故此对应不是映射.
对于选项C:集合B中5在集合A中对应两个数1,2,所以C是错误的.
故选D.
点评:本题考查映射的概念,即一个集合中的任何元素在另一个集合中都有唯一确定的一个元素和它对应,则此对应构成映射.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列从集合A到集合B的对应f是映射的是( )
A、 | B、 | C、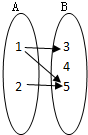 | D、 |
在下列从集合
A到集合B的对应关系中,不可以确定y是x的函数的是[
]①
A={x|xÎZ|,B= {y|yÎZ},对应法则②
A={x|x>0|,B= {y|yÎR},对应法则f:x®③
A={x|xÎR|,B= {y|yÎR},对应法则f:x®y= ;
;
|
A .① |
B .② |
C .③ |
D .①②③ |
 ;
; =2x;
=2x; ;
;