题目内容
直线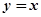 被曲线
被曲线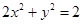 截得的弦长为 ;
截得的弦长为 ;
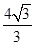
解析试题分析:联立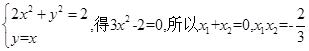 ,所以弦长为
,所以弦长为 。
。
考点:直线与椭圆的位置关系。
点评:本题主要考查弦长的求法,在求直线与圆锥曲线相交的弦长时一般采用韦达定理设而不求的方法,在求解过程中一般采取步骤为:设点→联立方程→消元→韦达定理→弦长公式。

练习册系列答案
相关题目
题目内容
直线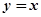 被曲线
被曲线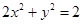 截得的弦长为 ;
截得的弦长为 ;
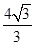
解析试题分析:联立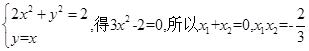 ,所以弦长为
,所以弦长为 。
。
考点:直线与椭圆的位置关系。
点评:本题主要考查弦长的求法,在求直线与圆锥曲线相交的弦长时一般采用韦达定理设而不求的方法,在求解过程中一般采取步骤为:设点→联立方程→消元→韦达定理→弦长公式。
