题目内容
设随机变量ξ的概率分布列为:P(ξ=k)=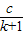 ,k=0,1,2,3,则P(ξ=2)= .
,k=0,1,2,3,则P(ξ=2)= .
【答案】分析:由题意可得P(ξ=0)+P(ξ=1)+P(ξ=2)+P(ξ=3)=1,所以c=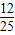 ,所以P(ξ=k)=
,所以P(ξ=k)=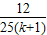 ,进而求出答案.
,进而求出答案.
解答:解:因为所有事件发生的概率之和为1,
即P(ξ=0)+P(ξ=1)+P(ξ=2)+P(ξ=3)=1,
所以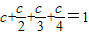 ,所以c=
,所以c=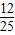 .
.
所以P(ξ=k)=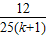 ,所以P(ξ=2)=
,所以P(ξ=2)=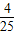 .
.
故答案为: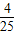 .
.
点评:解决此类问题的关键是掌握所有事件发生的概率之和为1,进而求出随机变量的分布列即可得到答案.
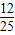 ,所以P(ξ=k)=
,所以P(ξ=k)=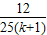 ,进而求出答案.
,进而求出答案.解答:解:因为所有事件发生的概率之和为1,
即P(ξ=0)+P(ξ=1)+P(ξ=2)+P(ξ=3)=1,
所以
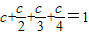 ,所以c=
,所以c=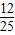 .
.所以P(ξ=k)=
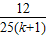 ,所以P(ξ=2)=
,所以P(ξ=2)=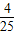 .
.故答案为:
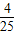 .
.点评:解决此类问题的关键是掌握所有事件发生的概率之和为1,进而求出随机变量的分布列即可得到答案.

练习册系列答案
相关题目
 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
. =5的概率;
=5的概率; (k=1,2,3,4):
(k=1,2,3,4): 的值;
的值; 的分布列;
的分布列; 的值.
的值.