题目内容
将7个人(含甲、乙)分成三个组,一组3人,另两组2人,不同的分组数为a,甲、乙分到同一组的概率为p,则a、p的值分别为( )
A、a=105 p=
| ||
B、a=105 p=
| ||
C、a=210 p=
| ||
D、a=210 p=
|
分析:本题是一道平均分组问题,将7个人(含甲、乙)分成三个组,一组3人,另两组2人,有两个组都是两个人,而这两个组又没有区别,所以分组数容易重复,甲、乙分到同一组的概率要分类计算.
解答:解:a=
=105
甲、乙分在同一组的方法种数有
(1)若甲、乙分在3人组,有
=15种
(2)若甲、乙分在2人组,有C53=10种,故共有25种,
所以P=
=
故选A
| ||||||
| 2! |
甲、乙分在同一组的方法种数有
(1)若甲、乙分在3人组,有
| ||||||
| 2! |
(2)若甲、乙分在2人组,有C53=10种,故共有25种,
所以P=
| 25 |
| 105 |
| 5 |
| 21 |
故选A
点评:平均分组问题是概率中最困难的问题,解题时往往会忽略有些情况是相同的,若4人分成两组,则有
种分法.
| ||||
| 2! |

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
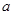 ,甲、乙分到同一组的概率为
,甲、乙分到同一组的概率为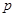 ,则
,则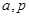 的值分别为
的值分别为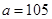 ,
,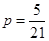 B.
B.
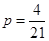
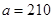 ,
, ,甲、乙分在同一组的概率为
,甲、乙分在同一组的概率为 ,则
,则 的值分别是( )
的值分别是( ) B、
B、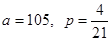
 D、
D、