题目内容
已知分别以d1和d2为公差的等差数列和满足a1=18,b14=36.(1)若d1=18,且存在正整数m,使得am2=bm+14-45,求证:d2>108;
(2)若ak=bk=0,且数列a1,a2,…,ak,bk+1,bk+2,…,b14的前n项和Sn满足S14=2Sk,求数列{an}和{bn}的通项公式.
分析:(1)根据等差数列的通项公式分别表示出am和bm+14,代入am2=bm+14-45,求得d2=182m+
,根据均值不等式求得d2的范围,原式得证.
(2)根据S14=2Sk得:Sk=S14-Sk,再根据等差数列的求和公式,进而求得d1和d2,根据等差数列的通项公式进而求得an和bn的通项公式.
| 9 |
| m |
(2)根据S14=2Sk得:Sk=S14-Sk,再根据等差数列的求和公式,进而求得d1和d2,根据等差数列的通项公式进而求得an和bn的通项公式.
解答:解:(1)依题意,[18+(m-1)×18]2=36+(m+14-14)d2-45,
即(18m)2=md2-9,即d2=182m+
≥2
=108;
等号成立的条件为182m=
,即m=
,∵m∈N*,
∴等号不成立,∴原命题成立.
(2)由S14=2Sk得:Sk=S14-Sk,
即:
×k=
×(14-k+1),
则9k=18×(15-k),得k=10
d1=
=-2,d2=
=9,
则an=-2n+20,bn=9n-90.
即(18m)2=md2-9,即d2=182m+
| 9 |
| m |
| 182×9 |
等号成立的条件为182m=
| 9 |
| m |
| 1 |
| 6 |
∴等号不成立,∴原命题成立.
(2)由S14=2Sk得:Sk=S14-Sk,
即:
| 18+0 |
| 2 |
| 36+0 |
| 2 |
则9k=18×(15-k),得k=10
d1=
| 0-18 |
| 9 |
| 36-0 |
| 14-10 |
则an=-2n+20,bn=9n-90.
点评:本题主要考查了等差数列的性质.属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
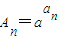 ,
,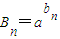 ,a>0且a≠1,探究不等式AnBn+1<An+Bn是否对一切正整数n恒成立?
,a>0且a≠1,探究不等式AnBn+1<An+Bn是否对一切正整数n恒成立?