题目内容
下列四个命题:①圆(x+2)2+(y+1)2=4与直线x-2y=0相交,所得弦长为2;
②直线y=kx与圆(x-cosθ)2+(y-sinθ)2=1恒有公共点;
③若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为108π;
④若棱长为
 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为 .
.其中,正确命题的序号为 .写出所有正确命的序号)
【答案】分析:①②是直线和圆的位置关系及弦长问题,一般转化为圆心到直线的距离问题,但本题中很容易看出①中直线x-2y=0过圆心,②中直线和圆均过原点;③④为与球有关的组合体问题,结合球的截面性质,球心与截面圆心的连线垂直于截面圆处理.
解答:解:①圆心(-2,-1)在直线x-2y=0上,即直线x-2y=0过圆心,所得弦长为直径4,结论错误;
②∵直线y=kx与圆(x-cosθ)2+(y-sinθ)2=1横过原点,故恒有公共点正确;
③球直径为正方体的对角线长即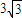 ,故求半径R=
,故求半径R=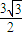 ,球表面积为s=4πR2=27π,结论错误;
,球表面积为s=4πR2=27π,结论错误;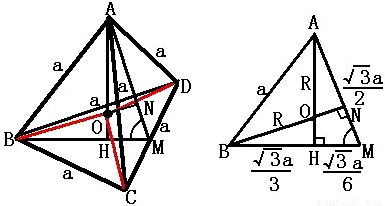
由上图可知,AH=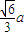 ,
,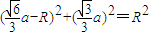 ,∴R=
,∴R=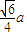 ,
,
∵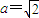 ,∴
,∴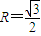 ,∴
,∴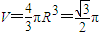 ,结论正确.
,结论正确.
故答案为:②④
点评:本题考查直线和圆的位置关系及与球有关的组合体问题.直线和圆的位置关系一般转化为圆心到直线的距离问题,与球有关的组合体问题要画好图形,结合球的截面性质.
解答:解:①圆心(-2,-1)在直线x-2y=0上,即直线x-2y=0过圆心,所得弦长为直径4,结论错误;
②∵直线y=kx与圆(x-cosθ)2+(y-sinθ)2=1横过原点,故恒有公共点正确;
③球直径为正方体的对角线长即
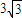 ,故求半径R=
,故求半径R=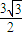 ,球表面积为s=4πR2=27π,结论错误;
,球表面积为s=4πR2=27π,结论错误;
由上图可知,AH=
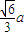 ,
,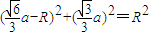 ,∴R=
,∴R=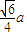 ,
,∵
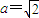 ,∴
,∴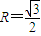 ,∴
,∴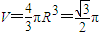 ,结论正确.
,结论正确.故答案为:②④
点评:本题考查直线和圆的位置关系及与球有关的组合体问题.直线和圆的位置关系一般转化为圆心到直线的距离问题,与球有关的组合体问题要画好图形,结合球的截面性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
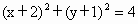 与直线x-2y=0相交,所得弦长为2;
与直线x-2y=0相交,所得弦长为2;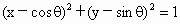 恒有公共点;
恒有公共点;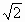 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为 ,其中,正确命题的代号为__________(按照原顺序写出所有正确命题的代号).
,其中,正确命题的代号为__________(按照原顺序写出所有正确命题的代号).