题目内容
设全集为U=R,函数f(x)=
的定义域为A,函数g(x)=x+1,(-2≤x<2)的值域为B.
(1)分别求集合A、B;
(2)求A∩(?UB).
| x2+2x-8 |
(1)分别求集合A、B;
(2)求A∩(?UB).
分析:(1)利用根式函数的定义域求出A,利用一次函数的值域求出B,
(Ⅱ)由∪=R,先求出CUB,由此能求出A∩(?UB).
(Ⅱ)由∪=R,先求出CUB,由此能求出A∩(?UB).
解答:解:(1)由x2+2x-8≥0得x≤-4或x≥2,∴A=(-∞,-4]∪[2,+∞),
∵-2≤x<2,∴-1≤x+1<3,B=[-1,3);端点值取错扣(1分),下同.
(2)?UB=(-∞,-1)∪[3,+∞),
∴A∩?UB=(-∞,-4]∪[3,+∞).
∵-2≤x<2,∴-1≤x+1<3,B=[-1,3);端点值取错扣(1分),下同.
(2)?UB=(-∞,-1)∪[3,+∞),
∴A∩?UB=(-∞,-4]∪[3,+∞).
点评:本题考查集合的交、并、补集的混合运算,解题时要认真审题,仔细解答,注意根式函数的定义域和一次函数的值域的合理运用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
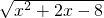 的定义域为A,函数g(x)=x+1,(-2≤x<2)的值域为B.
的定义域为A,函数g(x)=x+1,(-2≤x<2)的值域为B.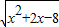 的定义域为A,函数g(x)=x+1,(-2≤x<2)的值域为B.
的定义域为A,函数g(x)=x+1,(-2≤x<2)的值域为B.