题目内容
设全集为U=R,集合A为函数f(x)=
+lg(3-x)-1的定义域,B={x|2x-4≥x-2}
(1)求A∪B,?U(A∩B)
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
| x+1 |
(1)求A∪B,?U(A∩B)
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
分析:(1)由二次根式的被开方数大于或等于0和对数的真数大于0,解不等式组得到集合A=[-1,3),结合集合B=[2,+∞)算出A∩B=[2,3),A∪B=[-1,+∞),再由全集补集的含义可求出?U(A∩B)的值.
(2)根据并集的性质得B?C,然后解出C=(-
,+∞),结合(1)中求出的集合B,建立关于a的不等式,解之即可得到实数a的取值范围.
(2)根据并集的性质得B?C,然后解出C=(-
| a |
| 2 |
解答:解:(1)解不等式组
,得-1≤x<3,
∴f(x)=
+lg(3-x)-1的定义域A=[-1,3),
又∵集合B={x|2x-4≥x-2}=[2,+∞),
∴A∩B=[2,3),A∪B=[-1,+∞),
∵全集为U=R,
∴?U(A∩B)=(-∞,2)∪[3,+∞),
综上所述,得A∪B=[-1,+∞),?U(A∩B)=(-∞,2)∪[3,+∞).
(2)由(1)得集合B=[2,+∞),
∵C={x|2x+a>0}=(-
,+∞),且B∪C=C,
∴B?C,可得-
<2,解之得a>-4.
即实数a的取值范围是(-4,+∞).
|
∴f(x)=
| x+1 |
又∵集合B={x|2x-4≥x-2}=[2,+∞),
∴A∩B=[2,3),A∪B=[-1,+∞),
∵全集为U=R,
∴?U(A∩B)=(-∞,2)∪[3,+∞),
综上所述,得A∪B=[-1,+∞),?U(A∩B)=(-∞,2)∪[3,+∞).
(2)由(1)得集合B=[2,+∞),
∵C={x|2x+a>0}=(-
| a |
| 2 |
∴B?C,可得-
| a |
| 2 |
即实数a的取值范围是(-4,+∞).
点评:本题给出集合A、B,求A、B的并集和交集的补集,并讨论了集合的包含关系,着重考查了函数定义域的求法和集合的基本运算等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 设全集为U=R,集合A={x|(x+3)(6-x)≤0},B={x|log2(x+2)<4}.
设全集为U=R,集合A={x|(x+3)(6-x)≤0},B={x|log2(x+2)<4}. 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|log2(x+2)<4}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|log2(x+2)<4}.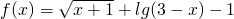 的定义域,B={x|2x-4≥x-2}
的定义域,B={x|2x-4≥x-2}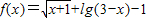 的定义域,B={x|2x-4≥x-2}
的定义域,B={x|2x-4≥x-2}