题目内容
已知曲线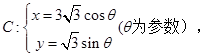 直线
直线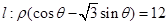
将直线 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
设点P在曲线C上,求点P到直线 的距离的最小值。
的距离的最小值。
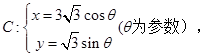 直线
直线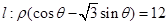
将直线
 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;设点P在曲线C上,求点P到直线
 的距离的最小值。
的距离的最小值。直线的直角坐标方程为 ,曲线C的普通方程为
,曲线C的普通方程为
点P到直线 的距离的最小值3.
的距离的最小值3.
 ,曲线C的普通方程为
,曲线C的普通方程为
点P到直线
 的距离的最小值3.
的距离的最小值3.试题分析:利用
 将曲线
将曲线 化为普通方程得
化为普通方程得 ,利用
,利用 将直线
将直线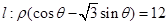 化为普通方程得
化为普通方程得 ,设与直线
,设与直线 平行的直线为
平行的直线为 ,当直线
,当直线 与椭圆
与椭圆 相切时,切点满足到直线的距离最小,联立直线曲线构成方程组,由
相切时,切点满足到直线的距离最小,联立直线曲线构成方程组,由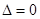 可求得c值,进而得到最小距离为3
可求得c值,进而得到最小距离为3点评:参数方程化普通方程只需将参数消去,常用加减消元或代入消元,极坐标与普通坐标的转化公式为
 ,在求点到直线的距离最小时结合图形转化为相切的平行线与已知直线的距离
,在求点到直线的距离最小时结合图形转化为相切的平行线与已知直线的距离
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
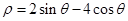 ,圆心为
,圆心为 ,直线
,直线 的参数方程为:
的参数方程为: (
(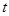 为参数),且直线
为参数),且直线 为 .
为 .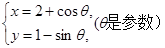 化为普通方程为 .
化为普通方程为 .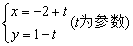 被圆
被圆 所截得的弦长为 .
所截得的弦长为 .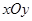 中,已知圆
中,已知圆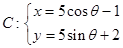 (
(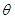 为参数)和直线
为参数)和直线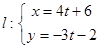 (
( 为参数),则直线
为参数),则直线 被圆C所截得弦长为 ;
被圆C所截得弦长为 ;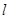 的参数方程是
的参数方程是 (t为参数)。以O为极点,x轴正方向为极轴的极坐标系中,曲线C的极坐标方程为
(t为参数)。以O为极点,x轴正方向为极轴的极坐标系中,曲线C的极坐标方程为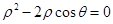 ,直线
,直线 ,点
,点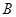 在直线
在直线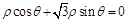 上运动,当线段
上运动,当线段 最短时,点
最短时,点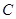 的参数方程为
的参数方程为
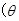 为参数), 以原点为极点,
为参数), 以原点为极点, 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为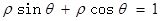 , 则直线
, 则直线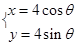 (
(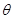 为参数)的弦,使M为弦的中点,则此弦所在直线的方程为( )
为参数)的弦,使M为弦的中点,则此弦所在直线的方程为( )


