题目内容
已知:数列{an}的前n项和为Sn,满足a1=1,当n∈N+时,Sn=an-n-1.(1)求a2,a3,a4;
(2)猜想an,并用数学归纳法证明你的猜想;
(3)已知

 ,求a的取值范围.
,求a的取值范围.
【答案】分析:(1)根据a1=1,当n∈N+时,Sn=an-n-1,可求得a2,a3,a4;
(2)猜想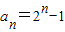 ,再用数学归纳法证明:当n=1时,经验证成立;假设当n=k,(k≥1)时结论成立,即
,再用数学归纳法证明:当n=1时,经验证成立;假设当n=k,(k≥1)时结论成立,即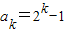 ,则当n=k+1时,有sk=ak+1-k-1;sk-1=ak-(k-1)-1,两式相减即可证得;
,则当n=k+1时,有sk=ak+1-k-1;sk-1=ak-(k-1)-1,两式相减即可证得;
(3) ,即
,即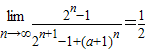 ,进而可得
,进而可得 ,从而可求a的取值范围.
,从而可求a的取值范围.
解答:解:(1)∵a1=1,当n∈N+时,Sn=an-n-1
∴S2=a2-3,∴a2=3;S3=a3-4,∴a3=7;S4=a4-5,∴a4=15
(2)猜想
证明:当n=1时,经验证成立
假设当n=k,(k≥1)时结论成立,即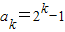
则当n=k+1时,有sk=ak+1-k-1;sk-1=ak-(k-1)-1,
两式相减得到ak=ak+1-ak-1,∴ak+1=2ak+1,∴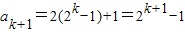
所以当n=k+1时,结论成立
综上所述: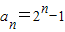
(3)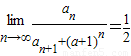 ,即
,即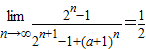
则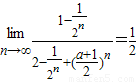 ,得到
,得到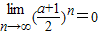
∴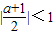
∴-3<a<-1
点评:本题考查数列递推式,考查数学归纳法的运用,考查数列的极限,掌握数学归纳法的证明方法是关键.
(2)猜想
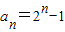 ,再用数学归纳法证明:当n=1时,经验证成立;假设当n=k,(k≥1)时结论成立,即
,再用数学归纳法证明:当n=1时,经验证成立;假设当n=k,(k≥1)时结论成立,即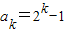 ,则当n=k+1时,有sk=ak+1-k-1;sk-1=ak-(k-1)-1,两式相减即可证得;
,则当n=k+1时,有sk=ak+1-k-1;sk-1=ak-(k-1)-1,两式相减即可证得;(3)
 ,即
,即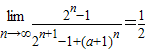 ,进而可得
,进而可得 ,从而可求a的取值范围.
,从而可求a的取值范围.解答:解:(1)∵a1=1,当n∈N+时,Sn=an-n-1
∴S2=a2-3,∴a2=3;S3=a3-4,∴a3=7;S4=a4-5,∴a4=15
(2)猜想

证明:当n=1时,经验证成立
假设当n=k,(k≥1)时结论成立,即
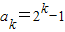
则当n=k+1时,有sk=ak+1-k-1;sk-1=ak-(k-1)-1,
两式相减得到ak=ak+1-ak-1,∴ak+1=2ak+1,∴
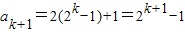
所以当n=k+1时,结论成立
综上所述:
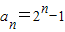
(3)
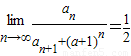 ,即
,即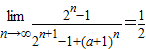
则
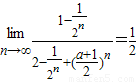 ,得到
,得到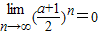
∴
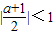
∴-3<a<-1
点评:本题考查数列递推式,考查数学归纳法的运用,考查数列的极限,掌握数学归纳法的证明方法是关键.

练习册系列答案
相关题目