题目内容
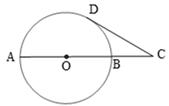
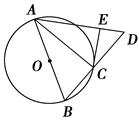
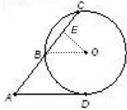
如下图,从圆O外一点A引圆的切线AD和割线ABC,已知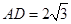 ,
,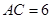 ,圆O的半径为3,则圆心O到AC的距离为 .
,圆O的半径为3,则圆心O到AC的距离为 .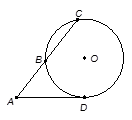

解析试题分析:要求圆心O到AC的距离,要先做出O点到AC的垂线段OE,则OE的长度即为所求,根据半径、半弦长(BE)、弦心距(OE)构成直角三角形,满足勾股定理,故要求出半弦长(BE),根据切割线定理,可以求出AB长,进而得到BE,代入即可,由题,如图,连接OB,过O点向AC引垂线,垂足为E,∵AD=2 ,AC=6,由切割线定理可得,AD2=AC•AB,∴AB=2,∴BC=4,由垂径定理得BE=2,又∵R=OB=3,∴OE=
,AC=6,由切割线定理可得,AD2=AC•AB,∴AB=2,∴BC=4,由垂径定理得BE=2,又∵R=OB=3,∴OE= .
.
考点:圆的切割线定理和垂径定理.

练习册系列答案
相关题目
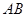 是圆
是圆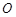 的直径,
的直径,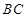 是圆
是圆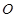 的切线,切点为
的切线,切点为 ,
, 平行于弦
平行于弦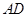 ,若
,若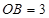 ,
,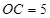 ,则
,则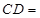 .
.
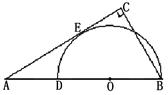
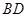 是半圆
是半圆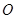 的直径,
的直径,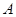 在
在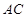 与半圆相切于点
与半圆相切于点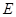 ,
, ,若
,若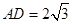 ,
,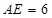 ,则
,则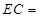 .
.
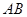 是圆
是圆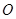 的直径,
的直径,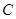 是
是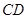 切圆
切圆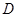 ,
,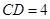 ,
,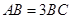 ,则圆
,则圆