题目内容
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=
,其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
|
分析:利润=收益-成本,由已知分两段当0≤x≤400时,和当x>400时,求出利润函数的解析式,分段求最大值,两者大着为所求利润最大值.
解答:解::由于月产量为x台,则总成本为20000+100x,从而利润f(x)=R(x)=
当0≤x≤400时,f(x)=-
(x-300)2+25000,
所以当x=300时,有最大值25000;
当x>400时,f(x)=60000-100x是减函数,
所以f(x)=60000-100×400<25000.
所以当x=300时,有最大值25000,
即当月产量为300台时,公司所获利润最大,最大利润是25000元.
|
当0≤x≤400时,f(x)=-
| 1 |
| 2 |
所以当x=300时,有最大值25000;
当x>400时,f(x)=60000-100x是减函数,
所以f(x)=60000-100×400<25000.
所以当x=300时,有最大值25000,
即当月产量为300台时,公司所获利润最大,最大利润是25000元.
点评:本题考查函数模型的应用:生活中利润最大化问题.函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.

练习册系列答案
相关题目
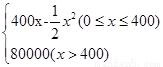 .
. ,其中
,其中 是仪器的月产量。
是仪器的月产量。 ;
; 总收益
总收益 总成本)
总成本) ,其中
,其中 是仪器的月产量.
是仪器的月产量. ;
;