题目内容
定义在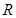 上的函数
上的函数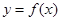 是奇函数,且满足
是奇函数,且满足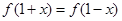 .当
.当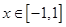 时,
时,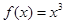 ,则
,则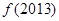 的值是( )
的值是( )
A.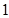 | B. | C. | D.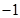 |
A
解析试题分析:因为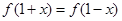 ,所以函数
,所以函数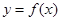 的对称轴是
的对称轴是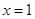 ,又函数
,又函数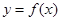 是奇函数,所以函数
是奇函数,所以函数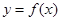 是以周期为
是以周期为 的周期函数.那么
的周期函数.那么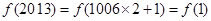 ,又当
,又当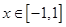 时,
时,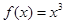 ,所以
,所以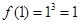 .
.
考点:函数性质的应用.

练习册系列答案
相关题目
若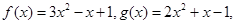 则
则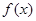 与
与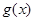 的大小关系是( )
的大小关系是( )
A.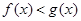 | B. |
C.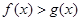 | D.随 的值的变化而变化 的值的变化而变化 |
设函数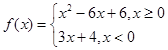 ,若互不相等的实数
,若互不相等的实数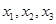 满足
满足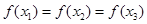 ,则
,则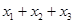 的取值范围是( )
的取值范围是( )
A.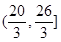 | B.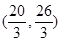 | C.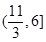 | D.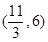 |
设 ,
, ,
, ,则( )
,则( )
| A.c>b>a | B.b>c>a | C.a>c>b | D.a>b>c |
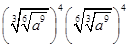 等于( )
等于( )
A.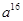 | B.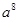 | C.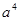 | D.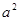 |
下列各式中成立的是( )
A.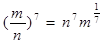 | B.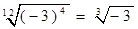 |
C.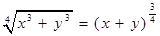 | D.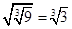 |
一支人数是5的倍数且不少于1000人的游行队伍,若按每横排4人编队,最后差3人;若按每横排3人编队,最后差2人;若按每横排2人编队,最后差1人.则这只游行队伍的最少人数是( )
| A.1025 | B.1035 | C.1045 | D.1055 |
已知 ,则
,则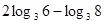 等于( )
等于( )
A.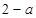 | B.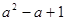 | C.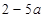 | D.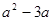 |
设 ,则
,则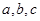 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |