题目内容
地球上最著名的几何物体莫过于埃及的吉沙(Giza)大金字塔,它的形状是正四棱锥.有着奇妙神秘的走道设计,以及神秘的密室.已知它的高度的2倍的平方等于它的侧面积.则侧面与底面所成的二面角的余弦值为分析:设出大金字塔的底面棱长为2a,高为h,根据正四棱锥的结构特征表达出侧面积与高的关系,即可得到
=
,再利用a与h表示出侧面与底面所成的二面角的余弦值,进而即可得到答案.
| h2 |
| a2 |
1+
| ||
| 2 |
解答: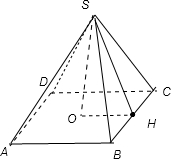 解:设大金字塔的底面棱长为2a,高为h,如图所示
解:设大金字塔的底面棱长为2a,高为h,如图所示
取BC的中点为H,O为正方形的中心,连接SO,OH,SH,
在正四棱锥中,SH⊥BC,OH⊥BC,所以∠SHO是侧面与底面所成的二面角.
则由题意可得其侧高SH=
,
因为它的高度的2倍的平方等于它的侧面积,即4×
×2a×
=4h2,
所以整理可得h4-a2h2-a4=0,即
=
.
所以在△SOH中,cos∠SHO=
=
=
≈0.618.
故答案为0.618.
 解:设大金字塔的底面棱长为2a,高为h,如图所示
解:设大金字塔的底面棱长为2a,高为h,如图所示取BC的中点为H,O为正方形的中心,连接SO,OH,SH,
在正四棱锥中,SH⊥BC,OH⊥BC,所以∠SHO是侧面与底面所成的二面角.
则由题意可得其侧高SH=
| a2+h2 |
因为它的高度的2倍的平方等于它的侧面积,即4×
| 1 |
| 2 |
| a2+h2 |
所以整理可得h4-a2h2-a4=0,即
| h2 |
| a2 |
1+
| ||
| 2 |
所以在△SOH中,cos∠SHO=
| OH |
| SH |
| a | ||
|
| 1 | ||||
|
故答案为0.618.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,根据其特征得到线段的关系并且表示出二面角的余弦,结合正确的运算进而解决问题.

练习册系列答案
相关题目