题目内容
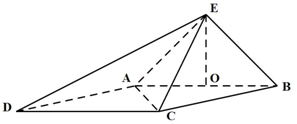 (2012•邯郸一模)已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=
(2012•邯郸一模)已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=| 2 |
(Ⅰ)求证:EO⊥平面ABCD;
(Ⅱ)求点D到面AEC的距离.
分析:(I)连接CO,利用△AEB为等腰直角三角形,证明EO⊥AB,利用勾股定理,证明EO⊥CO,利用线面垂直的判定,可得EO⊥平面ABCD;
(II)利用等体积,即VD-AEC=VE-ADC,从而可求点D到面AEC的距离.
(II)利用等体积,即VD-AEC=VE-ADC,从而可求点D到面AEC的距离.
解答: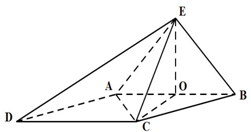 (I)证明:连接CO
(I)证明:连接CO
∵AE=EB=
,AB=2
∴△AEB为等腰直角三角形
∵O为AB的中点,∴EO⊥AB,EO=1…(2分)
又∵AB=BC,∠ABC=60°,∴△ACB是等边三角形
∴CO=
,…(4分)
又EC=2,∴EC2=EO2+CO2,
∴EO⊥CO,
∵AB∩CO=O
∴EO⊥平面ABCD…(6分)
(II)解:设点D到面AEC的距离为h
∵AE=
,AC=EC=2
∴S△AEC=
…(8分)
∵S△ADC=
,E到面ACB的距离EO=1,VD-AEC=VE-ADC
∴S△AEC•h=S△ADC•EO…(10分)
∴h=
∴点D到面AEC的距离为
…(12分)
 (I)证明:连接CO
(I)证明:连接CO∵AE=EB=
| 2 |
∴△AEB为等腰直角三角形
∵O为AB的中点,∴EO⊥AB,EO=1…(2分)
又∵AB=BC,∠ABC=60°,∴△ACB是等边三角形
∴CO=
| 3 |
又EC=2,∴EC2=EO2+CO2,
∴EO⊥CO,
∵AB∩CO=O
∴EO⊥平面ABCD…(6分)
(II)解:设点D到面AEC的距离为h
∵AE=
| 2 |
∴S△AEC=
| ||
| 2 |
∵S△ADC=
| 3 |
∴S△AEC•h=S△ADC•EO…(10分)
∴h=
2
| ||
| 7 |
∴点D到面AEC的距离为
2
| ||
| 7 |
点评:本题考查线面垂直,考查点到面距离的计算,解题的关键是掌握线面垂直的判定方法,考查等体积的运用,属于中档题.

练习册系列答案
相关题目
 (2012•邯郸一模)阅读如图的程序框图.若输入n=6,则输出k的值为( )
(2012•邯郸一模)阅读如图的程序框图.若输入n=6,则输出k的值为( ) (2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=
(2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=