题目内容
直线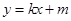
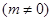 与椭圆
与椭圆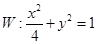 相交于
相交于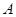 ,
,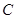 两点,
两点,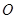 为坐标原点.
为坐标原点.
(Ⅰ)当点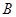 的坐标为
的坐标为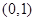 ,且四边形
,且四边形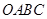 为菱形时,求
为菱形时,求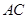 的长;
的长;
(Ⅱ)当点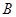 在
在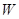 上且不是
上且不是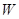 的顶点时,证明:四边形
的顶点时,证明:四边形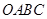 不可能为菱形.
不可能为菱形.
【答案】
利用椭圆的对称性,结合图形完成第(I)小题.设出直线方程,把直线方程和椭圆方程联立,设而不求,结合菱形的特点进行判断.
【解析】 (I) 椭圆W: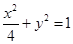 的右顶点
的右顶点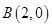 ,因为四边形OABC为菱形,所以
,因为四边形OABC为菱形,所以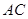 和
和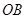 互相垂直平分.
互相垂直平分.
所以可设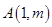 ,代入椭圆方程得
,代入椭圆方程得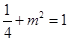 ,解得
,解得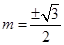 .
.
所以菱形OABC的面积为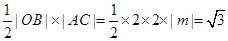 .
.
(II)假设四边形OABC为菱形.
因为点B不是W的顶点,且直线AC不过原点,所以可设AC的方程为y=kx+m,k≠0,m≠0..
由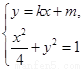 消去y并整理得
消去y并整理得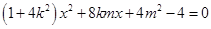 .
.
设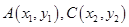 ,则
,则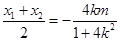 ,
,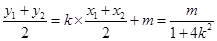 ,
,
所以AC的中点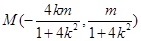 .
.
因为M为AC和OB的交点,所以直线OB的斜率为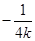 .
.
因为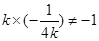 ,所以AC和OB不垂直.
,所以AC和OB不垂直.
所以四边形OABC不是菱形,与假设矛盾.
所以当B不是W的顶点,四边形OABC不可能是菱形.
【考点定位】本题考查了椭圆的性质和直线与椭圆的位置关系.通过整体代换,设而不求,考查了数据处理能力和整体思想的应用.

练习册系列答案
相关题目
 (2013•威海二模)已知椭圆
(2013•威海二模)已知椭圆