题目内容
已知 成等差数列.又数列an(an>0)中a1=3此数列的前n项的和Sn(n∈N+)对所有大于1的正整数n都有Sn=f(Sn-1).
成等差数列.又数列an(an>0)中a1=3此数列的前n项的和Sn(n∈N+)对所有大于1的正整数n都有Sn=f(Sn-1).(1)求数列an的第n+1项;
(2)若
 是
是 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.
【答案】分析:(1)有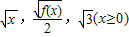 成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;
成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;
(2)由于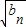 是
是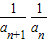 的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn.
的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn.
解答:解:(1)∵ 成等差数列,
成等差数列,
∴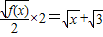 ∴
∴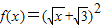 ∵Sn=f(Sn-1)(n≥2),∴
∵Sn=f(Sn-1)(n≥2),∴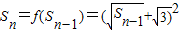
∴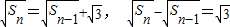
∴{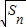 }是以
}是以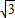 为公差的等差数列.
为公差的等差数列.
∵a1=3∴S1=3,∴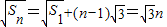 ,
,
∴Sn=3n2(n∈N+)
∴an+1=Sn+1-Sn=3(n+1)2-3n2=6n+3;
(2)∵数列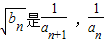 的等比中项,
的等比中项,
∴
∴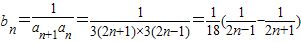
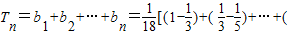
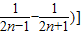 =
=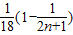
点评:此题考查了已知数列的前n项和求通项,等差数列的定义及等比中项,还考查了裂项相消法求数列的前n项的和.
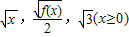 成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;
成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;(2)由于
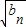 是
是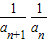 的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn.
的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn.解答:解:(1)∵
 成等差数列,
成等差数列,∴
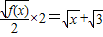 ∴
∴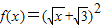 ∵Sn=f(Sn-1)(n≥2),∴
∵Sn=f(Sn-1)(n≥2),∴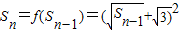
∴
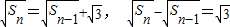
∴{
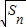 }是以
}是以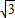 为公差的等差数列.
为公差的等差数列.∵a1=3∴S1=3,∴
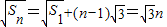 ,
,∴Sn=3n2(n∈N+)
∴an+1=Sn+1-Sn=3(n+1)2-3n2=6n+3;
(2)∵数列
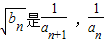 的等比中项,
的等比中项,∴

∴
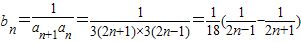
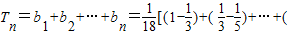
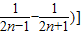 =
=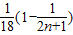
点评:此题考查了已知数列的前n项和求通项,等差数列的定义及等比中项,还考查了裂项相消法求数列的前n项的和.

练习册系列答案
相关题目
