题目内容

（理）曲线y=
x
与x=1，x=4，y=0所围成图形面积为
14
3
14
3
．
分析：由图形可知求出x从1到4，函数y=
x
上的定积分即为曲线y=
x
与x=1，x=4，y=0所围成的封闭图形的面积．
解答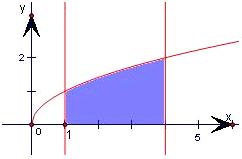：解：由定积分在求面积中的应用可知，
曲线y=
x
与x=1，x=4，y=0所围成的封闭图形的面积设为S，
则S=∫14（
x
-0）dx=
2
3
x
3
2
|14=
2
3
×4
3
2
-
2
3
×1
3
2
=
14
3
，
故答案为：
14
3
．
点评：考查学生会利用定积分求平面图形面积，会利用数形结合的数学思想来解决实际问题．
练习册系列答案
相关题目
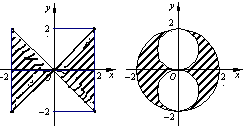精英家教网（理）由曲线y=|x|，y=-|x|，x=2，x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1；满足x2+y2≤4，x2+（y-1）2≥1，x2+（y+1）2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2，试写出V1与V2的一个关系式V1：V2=
 
．
（2008•杨浦区二模）（理）在平面直角坐标系xoy中，若在曲线C1的方程F（x，y）=0中，以（λx，λy）（λ为正实数）代替（x，y）得到曲线C2的方程F（λx，λy）=0，则称曲线C1、C2关于原点“伸缩”，变换（x，y）→（λx，λy）称为“伸缩变换”，λ称为伸缩比．
（1）已知曲线C1的方程为
x2
9
-
y2
4
=1，伸缩比λ=2，求C1关于原点“伸缩变换”后所得曲线C2的方程；
（2）射线l的方程y=
2
2
x(x≥0)，如果椭圆C1：
x2
16
+
y2
4
=1经“伸缩变换”后得到椭圆C2，若射线l与椭圆C1、C2分别交于两点A、B，且|AB|=
2
，求椭圆C2的方程；
（3）对抛物线C1：y2=2p1x，作变换（x，y）→（λ1x，λ1y），得抛物线C2：y2=2p2x；对C2作变换（x，y）→（λ2x，λ2y）得抛物线C3：y2=2p3x，如此进行下去，对抛物线Cn：y2=2pnx作变换（x，y）→（λnx，λny），得抛物线Cn+1：y2=2pn+1x，…．若p1=1 ， λn=(
1
2
)n，求数列{pn}的通项公式pn．

（04年浙江卷理）设曲线y=e-x(x≥0)在点M(t,e-t}处的切线l与x轴、y轴围成的三角形面积为S(t).
(1)求切线l的方程；
(2)求S(t)的最大值。
（理）由曲线y=|x|，y=-|x|，x=2，x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1；满足x2+y2≤4，x2+（y-1）2≥1，x2+（y+1）2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2，试写出V1与V2的一个关系式V1：V2=    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网