题目内容
2.函数f(x)=|x-1|-|x+1|,g(x)=ax2+bx+c(a≠0).(I)求不等式|f(x)|≤2的解集;
(Ⅱ)若不等式f(x)≥g(x)的解集与函数f(x)的值域相同,求x轴被曲线y=g(x)截得的弦的长度的取值范围.
分析 (I)化简f(x)=|x-1|-|x+1|=$\left\{\begin{array}{l}{2,x≤-1}\\{-2x,-1<x<1}\\{-2,x≥1}\end{array}\right.$,从而可得不等式|f(x)|≤2恒成立,
(Ⅱ)可得不等式f(x)≥g(x)的解集为[-2,2];从而可得$\left\{\begin{array}{l}{a>0}\\{g(-2)=4a-2b+c=2}\\{g(2)=4a+2b+c=-2}\\{g(1)=a+b+c≤-2}\\{-2≤-\frac{b}{2a}≤2}\end{array}\right.$,从而解得.
解答  解:(I)∵f(x)=|x-1|-|x+1|=$\left\{\begin{array}{l}{2,x≤-1}\\{-2x,-1<x<1}\\{-2,x≥1}\end{array}\right.$,
解:(I)∵f(x)=|x-1|-|x+1|=$\left\{\begin{array}{l}{2,x≤-1}\\{-2x,-1<x<1}\\{-2,x≥1}\end{array}\right.$,
∴不等式|f(x)|≤2恒成立,
即不等式|f(x)|≤2的解集为R;
(Ⅱ)∵函数f(x)的值域为[-2,2],
∴不等式f(x)≥g(x)的解集为[-2,2];
作辅助图象如右图,
∴$\left\{\begin{array}{l}{a>0}\\{g(-2)=4a-2b+c=2}\\{g(2)=4a+2b+c=-2}\\{g(1)=a+b+c≤-2}\\{-2≤-\frac{b}{2a}≤2}\end{array}\right.$,
解得,b=-1,c=-4a;a≥$\frac{1}{3}$;
故g(x)=ax2-x-4a,(a≥$\frac{1}{3}$);
设与x轴的两个交点的坐标为(m,0),(n,0);
则m+n=$\frac{1}{a}$,mn=-4;
∴(m-n)2=(m+n)2-4mn=$\frac{1}{{a}^{2}}$+16,
又∵0<$\frac{1}{{a}^{2}}$≤9,
∴16<16+$\frac{1}{{a}^{2}}$≤25,
∴x轴被曲线y=g(x)截得的弦的长度的取值范围为(4,5].
点评 本题考查了分段函数的应用及数形结合的思想应用,同时考查了不等式与函数的关系应用.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
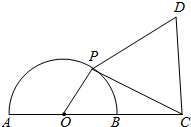 如图,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上一个动点,以DC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,则四边形OPDC面积的最大值为( )
如图,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上一个动点,以DC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,则四边形OPDC面积的最大值为( )| A. | 2 | B. | $\frac{5\sqrt{3}}{4}$-2 | C. | $\frac{5\sqrt{3}}{4}$ | D. | 2+$\frac{5\sqrt{3}}{4}$ |