题目内容
某种饮料分两次提价,提价方案有两种,方案甲:第一次提价p%,第二次提价q%;方案乙:每次都提价
%,若p>q>0,则提价多的方案是
| p+q | 2 |
乙
乙
.分析:两次提价属于增长率问题,分别计算出方案甲,方案乙增长后的价格,再比较大小.
解答:解:设提价前的价格为1,那么两次提价后的价格为,方案甲:(1+p%)(1+q%)=1+p%+q%+0.01pq%;
方案乙:(1+
%)(1+
%)=1+p%+q%+0.01×(
)2%;
∵(
)2≥pq,且p>q>0,∴上式“=”不成立;所以,方案乙提价最多.
故答案为乙.
方案乙:(1+
| p+q |
| 2 |
| p+q |
| 2 |
| p+q |
| 2 |
∵(
| p+q |
| 2 |
故答案为乙.
点评:本题考查了增长率问题和基本不等式的应用,是基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
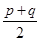 %,若p>q>0,则提价多的方案是 .
%,若p>q>0,则提价多的方案是 .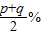 ,若p>q>0,则提价多的方案是 .
,若p>q>0,则提价多的方案是 . ,若p>q>0,则提价多的方案是 .
,若p>q>0,则提价多的方案是 .