题目内容
（本题满分12分）
如图所示，椭圆过点
，点
、
分别为椭圆的右焦点和右顶点
且有
（1）求椭圆的方程
（2）若动点
，符合条件：
，当
时，求证：动点一定在椭圆内部
|
|
 |
|
|
【答案】
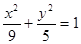
【解析】（1）依题意得：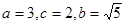
，
故椭圆的方程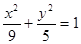（5分）
（2）由动点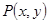
符合条件
，
、
、
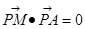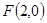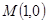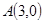得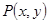的轨迹方程：
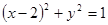，是以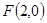为圆心，1为半径的圆。（8分）联立椭圆的方程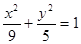得：公共点仅为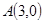又
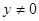所以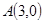舍去，从而该圆始终在椭圆内部。故动点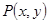一定在椭圆内部。（12分）
练习册系列答案
名校课堂系列答案
相关题目
是首项为
，公比
的等比数列，，
，数列
.
的通项公式；（2）求数列
的前n项和Sn.
<1，xÎR }．
，求实数a的取值范围．
（
，
为常数），且方程
有两个实根为
.
的解析式；
中，四边形
是边长为
的正方形，
，
为
上的点，且
⊥平面
⊥平面
的大小；
到平面