题目内容
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,曲线
,曲线![]() 上任意一点到
上任意一点到![]() 的距离等于该点到直线
的距离等于该点到直线![]() 的距离.
的距离.
(Ⅰ)求![]() 及曲线
及曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆只有一个交点
与椭圆只有一个交点![]() ,与曲线
,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ;(Ⅱ)0.
;(Ⅱ)0.
【解析】
解:(Ⅰ)由题意得![]() ,则
,则![]() ,设
,设![]() 为曲线
为曲线![]() 上任意一点,由题意得
上任意一点,由题意得![]() ,化简即可;
,化简即可;
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,![]() ,联立直线与椭圆方程并消元,可求得
,联立直线与椭圆方程并消元,可求得![]() ,且
,且![]() ,联立直线与曲线
,联立直线与曲线![]() 的方程消元,可得
的方程消元,可得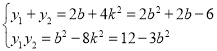 , 而
, 而![]() ,
,![]() ,根据三角形面积公式,将数据代入到
,根据三角形面积公式,将数据代入到![]() 即可求出结论.
即可求出结论.
解:(Ⅰ)由![]() 知该椭圆的焦点在
知该椭圆的焦点在![]() 轴上,
轴上,
∴![]() ,解得
,解得![]() ,
,
设![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,
由题意得![]() ,化简得
,化简得![]() ,
,
∴![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ;
;
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() ,
,
∵直线![]() 与椭圆只有一个交点
与椭圆只有一个交点![]() ,
,
∴![]() ,∴
,∴![]() ,
,
且![]() ,
,![]() ,①
,①
由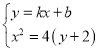 ,得
,得![]() ,
,
∴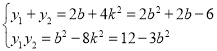 ,②
,②
由曲线![]() 的定义知
的定义知![]() ,
,![]() ,
,
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴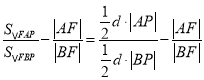
![]()
![]()
![]() ,
,
将①②代入分子![]()
![]()
![]() ,
,
∴![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目