题目内容
给出幂函数①f(x)=x;②f(x)=x2;③f(x)=x3;④f(x)=| x |
| 1 |
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
分析:对于①②分别求出平均数的函数值与函数值的平均数,比较出大小;对于③④⑤,有图象的上凸和下凸,画出图,比较出两者的大小.
解答:解:对于①有f(
)=
,
=
所以f(
)=
,故不满足;
对于②f(
)=
,
=
,
∴
-f(
)=
>0,故不满足;
对于③,其图象在第一象限的图象是向下凸的,所以有
>f(
),不满足条件;
对于④,其图象在第一象限是上凸的,所以有
<f(
),满足条件;
对于⑤,其图象在第一象限的图象是向下凸的,所以有
>f(
)不满足条件;
故答案为1
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
对于②f(
| x1+x2 |
| 2 |
| x12+2x1x2+x22 |
| 4 |
| f(x1)+f(x2) |
| 2 |
| x12+x22 |
| 2 |
∴
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x12-2x1x2+x22 |
| 4 |
对于③,其图象在第一象限的图象是向下凸的,所以有
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
对于④,其图象在第一象限是上凸的,所以有
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
对于⑤,其图象在第一象限的图象是向下凸的,所以有
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
故答案为1
点评:本题考查幂函数的图象、考查结合图象的上凸还是下凸,判断出平均数的函数值与函数值的平均数的大小.

练习册系列答案
相关题目
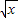 ;⑤f(x)=
;⑤f(x)=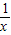 .其中满足条件f
.其中满足条件f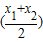 >
>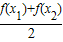 (x1>x2>0)的函数的个数是( )
(x1>x2>0)的函数的个数是( )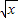 ;⑤f(x)=
;⑤f(x)=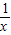 .其中满足条件f
.其中满足条件f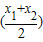 >
>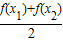 (x1>x2>0)的函数的个数是( )
(x1>x2>0)的函数的个数是( )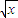 ;⑤f(x)=
;⑤f(x)=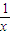 .其中满足条件f
.其中满足条件f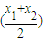 >
>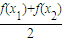 (x1>x2>0)的函数的个数是( )
(x1>x2>0)的函数的个数是( )