题目内容
给出幂函数①f(x)=x;②f(x)=x2;③f(x)=x3;④f(x)=
;⑤f(x)=
.其中满足条件f(
)>
(x1>x2>0)的函数的个数是( )
| x |
| 1 |
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:若函数满足f(
)>
(x1>x2>0)则表示函数在敬意(0,+∞)上是凸形的,分析题目中五个函数图象的形状,易得到结果.
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
解答:解:①函数f(x)=x的图象是一条直线,故当x1>x2>0时,f(
)=
;
②函数f(x)=x2的图象是凹形曲线,故当x1>x2>0时,f(
)<
;
③在第一象限,函数f(x)=x3的图象是凹形曲线,故当x1>x2>0时,f(
)<
;
④函数f(x)=
的图象是凸形曲线,故当x1>x2>0时,f(
)>
;
⑤在第一象限,函数f(x)=
的图象是一条直线,故当x1>x2>0时,f(
)=
;
故仅有函数f(x)=
满足,当x1>x2>0时,f(
)>
;
故选:A
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
②函数f(x)=x2的图象是凹形曲线,故当x1>x2>0时,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
③在第一象限,函数f(x)=x3的图象是凹形曲线,故当x1>x2>0时,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
④函数f(x)=
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
⑤在第一象限,函数f(x)=
| 1 |
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故仅有函数f(x)=
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故选:A
点评:本题考查的知识点是幂函数的图象和性质,其中准确理解f(
)>
(x1>x2>0)表示的几何意义是解答本题的关键.
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |

练习册系列答案
相关题目
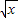 ;⑤f(x)=
;⑤f(x)=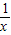 .其中满足条件f
.其中满足条件f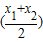 >
>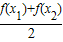 (x1>x2>0)的函数的个数是( )
(x1>x2>0)的函数的个数是( )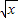 ;⑤f(x)=
;⑤f(x)=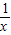 .其中满足条件f
.其中满足条件f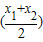 >
>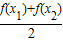 (x1>x2>0)的函数的个数是( )
(x1>x2>0)的函数的个数是( )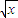 ;⑤f(x)=
;⑤f(x)=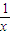 .其中满足条件f
.其中满足条件f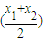 >
>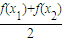 (x1>x2>0)的函数的个数是( )
(x1>x2>0)的函数的个数是( )