题目内容
已知函数g(x)=x2-4x+5,函数f(x)=x3+ax2+bx+c在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,当且仅当x>4时,f(x)>g(x)
(1)求函数f(x)的解析式
(2)若y=m与函数g(x)的图象有3个公共点,求m的取值范围.
(1)求函数f(x)的解析式
(2)若y=m与函数g(x)的图象有3个公共点,求m的取值范围.
分析:(1)由函数f(x)=x3+ax2+bx+c在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,知函数f(x)在点x=-1或2处取得极值,可得f′(1)=0,f′(2)=0求导,即可求字母的值;
(2)由(1)知f(x)=x3-
x2-6x-11.作出其图象,如图,数形结合,若y=m与函数g(x)的图象有3个公共点,求m的取值范围.
(2)由(1)知f(x)=x3-
| 3 |
| 2 |
解答: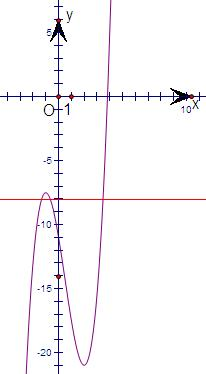 解:(1)f′(x)=3x2+2ax+b,
解:(1)f′(x)=3x2+2ax+b,
∵f(x)在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,
∴f′(-1)=0,f′(2)=0,
即f′(-1)=3-2ax+b=0,f′(2)=12+4ax+b=0,
∴a=-
,b=-6,;
又f(4)=g(4),⇒c=-11.
∴f(x)=x3-
x2-6x-11.
(2)由(1)知f(x)=x3-
x2-6x-11.
作出其图象,如图.
∵f(x)的图象与y=m的图象只有三个交点,
数形结合,m的取值范围:(-
,-21).
 解:(1)f′(x)=3x2+2ax+b,
解:(1)f′(x)=3x2+2ax+b,∵f(x)在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,
∴f′(-1)=0,f′(2)=0,
即f′(-1)=3-2ax+b=0,f′(2)=12+4ax+b=0,
∴a=-
| 3 |
| 2 |
又f(4)=g(4),⇒c=-11.
∴f(x)=x3-
| 3 |
| 2 |
(2)由(1)知f(x)=x3-
| 3 |
| 2 |
作出其图象,如图.
∵f(x)的图象与y=m的图象只有三个交点,
数形结合,m的取值范围:(-
| 15 |
| 2 |
点评:考查应用导数研究函数的极值和单调性问题,有关函数图象交点个数问题,转化为图象交点的个数问题,体现了转化的思想方法,属中档题.

练习册系列答案
相关题目
已知函数f(x)、g(x),下列说法正确的是( )
| A、f(x)是奇函数,g(x)是奇函数,则f(x)+g(x)是奇函数 | B、f(x)是偶函数,g(x)是偶函数,则f(x)+g(x)是偶函数 | C、f(x)是奇函数,g(x)是偶函数,则f(x)+g(x)一定是奇函数或偶函数 | D、f(x)是奇函数,g(x)是偶函数,则f(x)+g(x)可以是奇函数或偶函数 |