题目内容
设A、B为双曲线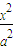 -
-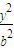 =1同一条渐近线上的两个不同的点,若|AB|=6,
=1同一条渐近线上的两个不同的点,若|AB|=6, 在向量m=(1,0)上的射影为3,则双曲线的离心率e等于( )
在向量m=(1,0)上的射影为3,则双曲线的离心率e等于( )A.2
B.
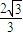
C.2或
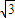
D.2或
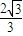
【答案】分析:利用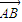 在x轴上的射影长和|AB|求得A、B点所在的渐近线与x轴的夹角,a和b的关系,利用c2=a2+b2求得c和a的关系,则双曲线的离心率可得.
在x轴上的射影长和|AB|求得A、B点所在的渐近线与x轴的夹角,a和b的关系,利用c2=a2+b2求得c和a的关系,则双曲线的离心率可得.
解答:解: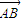 在x轴上的射影长为3
在x轴上的射影长为3
而|AB|=6,因此A、B点所在的渐近线与x轴的夹角为60°.
有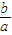 =tan60°⇒b=
=tan60°⇒b=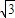 a
a
所以c2=a2+b2=4a2⇒e=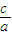 =2,
=2,
故选A
点评:本题主要考查了双曲线的简单性质.考查了学生平面解析几何的基础知识的掌握和灵活运用.
 在x轴上的射影长和|AB|求得A、B点所在的渐近线与x轴的夹角,a和b的关系,利用c2=a2+b2求得c和a的关系,则双曲线的离心率可得.
在x轴上的射影长和|AB|求得A、B点所在的渐近线与x轴的夹角,a和b的关系,利用c2=a2+b2求得c和a的关系,则双曲线的离心率可得.解答:解:
 在x轴上的射影长为3
在x轴上的射影长为3而|AB|=6,因此A、B点所在的渐近线与x轴的夹角为60°.
有
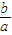 =tan60°⇒b=
=tan60°⇒b=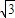 a
a所以c2=a2+b2=4a2⇒e=
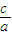 =2,
=2,故选A
点评:本题主要考查了双曲线的简单性质.考查了学生平面解析几何的基础知识的掌握和灵活运用.

练习册系列答案
相关题目
设A、B为双曲线
-
=1同一条渐近线上的两个不同的点,若|AB|=6,
在向量m=(1,0)上的射影为3,则双曲线的离心率e等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| A、2 | ||||
B、
| ||||
C、2或
| ||||
D、2或
|
设A、B为双曲线
-
=λ(λ≠0)同一条渐近线上的两个不同的点,已知向量
=(1,0),|
|=6,
=3,则双曲线的离心率e等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| m |
| AB |
| ||||
|
|
| A、2 | ||||
B、
| ||||
C、2或
| ||||
D、2或
|
 在向量
在向量 =(1,0)上的投影为3,则双曲线的离心率e等于 ( )
=(1,0)上的投影为3,则双曲线的离心率e等于 ( ) C.2或
C.2或 D.2或
D.2或