题目内容
已知函数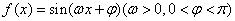 的一系列对应值如表:
的一系列对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求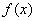 的解析式;
的解析式;
(2)若在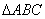 中,
中,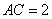 ,
,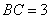 ,
,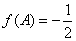 (A为锐角),求
(A为锐角),求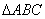 的面积.
的面积.
【答案】
(Ⅰ)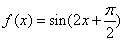 (或者
(或者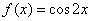 );
);
(Ⅱ)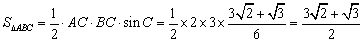 .
.
【解析】
试题分析:(Ⅰ)由题中表格给出的信息可知,函数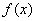 的周期为
的周期为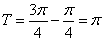 ,
,
所以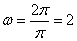 .
2分
.
2分
注意到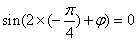 ,也即
,也即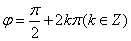 ,由
,由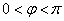 ,所以
,所以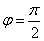 4分
4分
所以函数的解析式为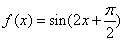 (或者
(或者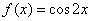 )
5分
)
5分
(Ⅱ)∵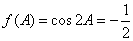 ,且A为锐角,∴
,且A为锐角,∴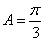 6分
6分
在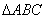 中,由正弦定理得,
中,由正弦定理得,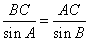 ,∴
,∴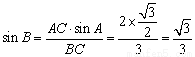 , 7分
, 7分
∵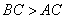 ,∴
,∴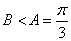 ,∴
,∴ , 8分
, 8分
∴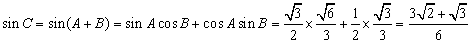 , 10分
, 10分
∴ . 12分
. 12分
考点:本题主要考查三角函数的图象和性质,和差倍半的三角函数,正弦定理的应用。
点评:中档题,利用图象或变量的对应值表确定函数的解析式,要明确A,T,进一步求 。计算三角形的面积,应围绕两边及其夹角的正弦思考,故利用正弦定理、和差倍半的三角函数,可使问题得解。
。计算三角形的面积,应围绕两边及其夹角的正弦思考,故利用正弦定理、和差倍半的三角函数,可使问题得解。

练习册系列答案
相关题目
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
(1)根据表格提供的数据求函数y=f(x)的解析式;
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0), 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
 的一系列对应值如下表:
的一系列对应值如下表:| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),
 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.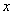
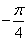
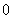
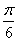
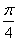
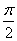
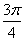

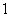
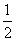
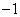
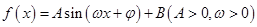 的一系列对应值如下表:
的一系列对应值如下表:







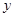



 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.  的一系列对应值如下表:
的一系列对应值如下表:






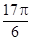



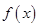 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.